题目内容
3.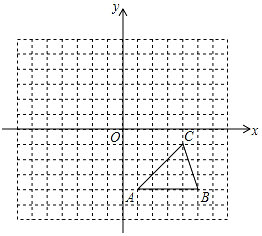 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2,并写出C2的坐标.
分析 ①直接利用位似图形的性质得出对应点位置进而得出答案;
②直接利用旋转的性质得出对应点位置,进而得出答案.
解答  解:①如图所示:△A1B1C1,即为所求,
解:①如图所示:△A1B1C1,即为所求,
C1的坐标为:(-8,2);
②如图所示:△A2B2C2,即为所求,
C2的坐标为:(-1,-4).
点评 此题主要考查了位似变换以及旋转变换,正确得出对应点位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设一元二次方程x2-2x-4=0的两个实根为x1和x2,则x12+x22=( )
| A. | -8 | B. | 8 | C. | -12 | D. | 12 |
8.为加强公民节水意识,合理利用水资源,某市采用如下水费计费方式:
(1)某用户4月用水12.5m3,应收水费多少元?
(2)如果该用户3、4月份共用水15m3(4月比3月多),共交水费44元,则该用户3、4月份各用水多少m3?
| 用水量 | 单价 |
| 不超过6m3 | 2元/m3 |
| 超过6m3不到10m3 | 4元m3 |
| 超出10m3 | 8元m3 |
(2)如果该用户3、4月份共用水15m3(4月比3月多),共交水费44元,则该用户3、4月份各用水多少m3?
 已知二次函数y=-x2-2x+3.
已知二次函数y=-x2-2x+3. 已知,如图1,点A、B分别在x轴、y轴正半轴上,∠OAB、∠OBA的平分线相交于点E,分别交x轴、y轴于点D、C.
已知,如图1,点A、B分别在x轴、y轴正半轴上,∠OAB、∠OBA的平分线相交于点E,分别交x轴、y轴于点D、C.