题目内容
12.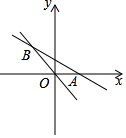 如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.
如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.(1)求点A、B的坐标;
(2)求△AOB的面积.
分析 (1)根据直线与x轴的坐标的特点,将y=0,代入解析式,即可求得点A的坐标;联立两条直线解析式组成方程组,求的方程组的解,即可得到点B的坐标;
(2)根据三角形的面积=底×高×$\frac{1}{2}$,即可求出三角形的面积.
解答 解:(1)由${y_1}=-\frac{1}{2}x+1$,可知当y=0时,x=2,
∴点A的坐标是(2,0)
∵${y_1}=-\frac{1}{2}x+1$与${y_2}=-\frac{3}{2}x$交于点B,$\left\{\begin{array}{l}y=-\frac{1}{2}x+1\\ y=-\frac{3}{2}x\end{array}\right.,解得\left\{\begin{array}{l}x=-1\\ y=1.5\end{array}\right.$
∴B点的坐标是(-1,1.5),
(2)∵AO=2,
∴△AOB的面积=$\frac{1}{2}$×2×1.5=1.5.
点评 本题主要考查两条直线的交点,解决此题时,明确二元一次方程组与一次函数的关系是解决此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列运算错误的是( )
| A. | -8-2×6=-20 | B. | (-1•)2015+(-1)2016=0 | ||
| C. | -(-3)2=-9 | D. | 2÷$\frac{4}{3}$×$\frac{3}{4}$=2 |
 如图,CA⊥AB,CA=AB,DA=AE,BD=CE,求证:DA⊥EA.
如图,CA⊥AB,CA=AB,DA=AE,BD=CE,求证:DA⊥EA. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是(0,4+2$\sqrt{2}$),Q点的坐标是(2$\sqrt{2}$+2,2$\sqrt{2}$+2).
如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是(0,4+2$\sqrt{2}$),Q点的坐标是(2$\sqrt{2}$+2,2$\sqrt{2}$+2).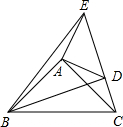 已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)-CD2,其中结论正确的个数是( )
已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)-CD2,其中结论正确的个数是( ) 如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是EF∥BC(写出一个即可)
如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是EF∥BC(写出一个即可) 如图是一个拦水大坝的横断面图,AD∥BC,如果背水坡AB的坡度为1:$\sqrt{3}$,则坡角∠B=30°.
如图是一个拦水大坝的横断面图,AD∥BC,如果背水坡AB的坡度为1:$\sqrt{3}$,则坡角∠B=30°. 如图,数轴上线段AB=2,CD=4,点A在数轴上表示的数是-10,点C在数轴上表示的数是16,若线段AB以6个单位/秒的速度向右匀速运动,同时线段CD以2个单位/秒的速度向左匀速运动.
如图,数轴上线段AB=2,CD=4,点A在数轴上表示的数是-10,点C在数轴上表示的数是16,若线段AB以6个单位/秒的速度向右匀速运动,同时线段CD以2个单位/秒的速度向左匀速运动.