题目内容
7. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是(0,4+2$\sqrt{2}$),Q点的坐标是(2$\sqrt{2}$+2,2$\sqrt{2}$+2).
如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是(0,4+2$\sqrt{2}$),Q点的坐标是(2$\sqrt{2}$+2,2$\sqrt{2}$+2).
分析 过P点作x轴的平行线交y轴于M,交AB于N,如图,设C(0,t),OP=2$\sqrt{2}$,OM=BN=PM=2,CM=t-2,利用旋转性质得PC=PD,∠CPD=90°,再证明△PCM≌△DPN得到PN=CM=2-t,DN=PM=2,于是得到D(t,4),接着利用△OPC≌△ADP得到AD=OP=2$\sqrt{2}$,则A(t,4+2$\sqrt{2}$),于是利用y=x图象上点的坐标特征得到t=4+2$\sqrt{2}$,所以C(0,4+2$\sqrt{2}$),D(4+2$\sqrt{2}$,4),接下来利用待定系数求出直线CD的解析式为y=(1-$\sqrt{2}$)x+4+2$\sqrt{2}$,则通过解方程组$\left\{\begin{array}{l}{y=x}\\{y=(1-\sqrt{2})x+4+2\sqrt{2}}\end{array}\right.$可得Q点坐标.
解答 解:过P点作x轴的平行线交y轴于M,交AB于N,如图,设C(0,t),
∴P(2,2),
∴OP=2$\sqrt{2}$,OM=BN=PM=2,CM=t-2,
∵线段PC绕点P顺时针旋转90°至线段PD,
∴PC=PD,∠CPD=90°,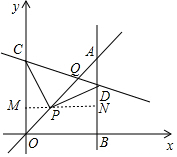
∴∠CPM+∠DPN=90°,
而∠CPM+∠PCM=90°,
∴∠PCM=∠DPN,
在△PCM和△DPN中
$\left\{\begin{array}{l}{∠PMC=∠DNP}\\{∠PCM=∠DPN}\\{PC=DP}\end{array}\right.$,
∴△PCM≌△DPN,
∴PN=CM=2-t,DN=PM=2,
∴MN=2-t+2=t,DB=2+2=4,
∴D(t,4),
∵△OPC≌△ADP,
∴AD=OP=2$\sqrt{2}$,
∴A(t,4+2$\sqrt{2}$),
把A(t,4+2$\sqrt{2}$)代入y=x得t=4+2$\sqrt{2}$,
∴C(0,4+2$\sqrt{2}$),D(4+2$\sqrt{2}$,4),
设直线CD的解析式为y=kx+b,
把C(0,4+2$\sqrt{2}$),D(4+2$\sqrt{2}$,4)代入得$\left\{\begin{array}{l}{b=4+2\sqrt{2}}\\{(4+2\sqrt{2})k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1-\sqrt{2}}\\{b=4+2\sqrt{2}}\end{array}\right.$,
∴直线CD的解析式为y=(1-$\sqrt{2}$)x+4+2$\sqrt{2}$,
解方程组$\left\{\begin{array}{l}{y=x}\\{y=(1-\sqrt{2})x+4+2\sqrt{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=2\sqrt{2}+2}\\{y=2\sqrt{2}+2}\end{array}\right.$,
∴Q(2$\sqrt{2}$+2,2$\sqrt{2}$+2).
故答案为(0,4+2$\sqrt{2}$),(2$\sqrt{2}$+2,2$\sqrt{2}$+2).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.会应用全等三角形证明线段相等,理解坐标与图形性质.

| 甲 | 乙 | |
| 进价(元/件) | 22 | 30 |
| 售价(元/件) | 29 | 40 |
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原售价销售,乙商品在原售价上打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元,求第二次乙种商品是按原价打几折销售?
 如图,正方形OABC的边长为4,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是( )
如图,正方形OABC的边长为4,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\frac{8}{3}$π | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{2}$ |
| A. | 2a2-2a+1=2a(a-1)+1 | B. | (x+y)(x-y)=x2-y2 | ||
| C. | x2-6x+5=(x-5)(x-1) | D. | x2+y2=(x-y)2+2xy |
 如图,在菱形ABCD中,E为AD边的中点,BE与对角线AC交于点F,过点F作FG⊥AB,垂足为点G.
如图,在菱形ABCD中,E为AD边的中点,BE与对角线AC交于点F,过点F作FG⊥AB,垂足为点G. 某校为了了解七年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制了图中所示的频数分布直方图,请根据图示计算,仰卧起坐次数在15-20(不含20)次的频数是3.
某校为了了解七年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制了图中所示的频数分布直方图,请根据图示计算,仰卧起坐次数在15-20(不含20)次的频数是3.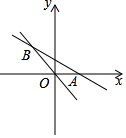 如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.
如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.