题目内容
 如图,AD是△ABC的中线,F是AC上一点.且CF=2AF,连接BF交AD于点E.求证:BE=3EF.
如图,AD是△ABC的中线,F是AC上一点.且CF=2AF,连接BF交AD于点E.求证:BE=3EF.考点:平行线分线段成比例
专题:证明题
分析:首先过点D作DG∥BF,交AC于G,作DH∥AC,交BF于点H,再根据平行线分线段成比例定理可得
=
=
,然后证明△EHD≌△EFA可得HE=EF,进而得到BE=3EF.
| FG |
| FC |
| BD |
| BC |
| 1 |
| 2 |
解答:证明:过点D作DG∥BF,交AC于G,作DH∥AC,交BF于点H,
∵DH∥AC,DG∥BF,
∴四边形HDGF是平行四边形,
∴HD=FG,DG=HF,
∵AD是△ABC的中线,
∴DB=DC=
BC,DH=
FC,
∵DH∥FC,D为BC中点,
∴BH=HF,
∵DG∥BF,
∴
=
=
,
∴G为BF中点,
∴DG是△BFC的中位线,
∴FC=2GC=2FG=2HD,
∵CF=2AF,
∴HD=AF,
在△EHD和△EFA中
,
∴△EHD≌△EFA(AAS),
∴HE=EF,
∴BE=3EF.
∵DH∥AC,DG∥BF,
∴四边形HDGF是平行四边形,
∴HD=FG,DG=HF,
∵AD是△ABC的中线,
∴DB=DC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DH∥FC,D为BC中点,
∴BH=HF,
∵DG∥BF,
∴
| FG |
| FC |
| BD |
| BC |
| 1 |
| 2 |
∴G为BF中点,
∴DG是△BFC的中位线,

∴FC=2GC=2FG=2HD,
∵CF=2AF,
∴HD=AF,
在△EHD和△EFA中
|
∴△EHD≌△EFA(AAS),
∴HE=EF,
∴BE=3EF.
点评:此题主要考查了平行线分线段成比例定理,以及全等三角形的判定与性质,关键是证明△EHD≌△EFA.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 反比例函数的图象如图,点M(1,3)和点N(3,1)在反比例函数的图象上,则△OMN的面积为( )
反比例函数的图象如图,点M(1,3)和点N(3,1)在反比例函数的图象上,则△OMN的面积为( )| A、3 | B、4 | C、5 | D、6 |
 线段AD=12cm,线段AC=BD=8cm,E、F分别是线段AB、CD中点,求EF.
线段AD=12cm,线段AC=BD=8cm,E、F分别是线段AB、CD中点,求EF.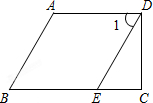 如图,AD∥BC,∠1=∠B.
如图,AD∥BC,∠1=∠B.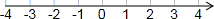 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题: