题目内容
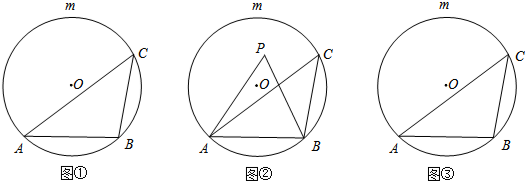
12. 在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;(2)分别以D,E为圆心,以大于$\frac{1}{2}$DE的同样长为半径作弧,两弧交于点C;
(3)作射线OC.
则OC就是所求作的射线.
小明同学想知道为什么这样做,所得到射线OC就是∠AOB的平分线.
小华的思路是连接DC、EC,可证△ODC≌△OEC,就能得到∠AOC=∠BOC.其中证明△ODC≌△OEC的理由是SSS.
分析 由作法可知:CD=CE,OD=OE,根据全等三角形的判定定理判断即可.
解答 解:由作法可知:CD=CE,OD=OE,
又∵OC=OC,
∴根据SSS可推出△OCD和△OCE全等,
故答案为:SSS
点评 本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
17.下图中不能表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
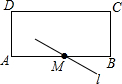 如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm.
如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm. 如图,△ABO≌△CDO,点E、F在线段AC上,且AF=CE.求证:FD=BE.
如图,△ABO≌△CDO,点E、F在线段AC上,且AF=CE.求证:FD=BE.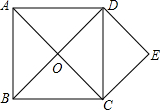 如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.
如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.