题目内容
 如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )A、100
| ||
| B、200 | ||
| C、100 | ||
D、200
|
考点:解直角三角形的应用-方向角问题
专题:
分析:先根据方向角的定义得出∠CAB=30°,∠ABC=120°,由三角形内角和定理求出∠C=180°-∠CAB-∠ABC=30°,则∠CAB=∠C=30°,根据等角对等边求出BC=AB=200m.
解答:解:如图,由题意得∠CAB=30°,∠ABC=90°+30°=120°,
∴∠C=180°-∠CAB-∠ABC=30°,
∴∠CAB=∠C=30°,
∴BC=AB=200m,
即景点B、C相距的路程为200m.
故选B.
∴∠C=180°-∠CAB-∠ABC=30°,
∴∠CAB=∠C=30°,
∴BC=AB=200m,
即景点B、C相距的路程为200m.
故选B.
点评:本题考查解直角三角形的应用-方向角问题,比较简单.涉及到三角形内角和定理,等腰三角形的判定等知识.根据条件得出∠CAB=∠C是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1纳米等于1米的10亿分之一,下列可以表示小明身高的是( )
| A、1.4×10-8纳米 |
| B、1.4×10-9纳米 |
| C、1.4×108纳米 |
| D、1.4×109纳米 |
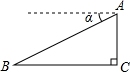 在寻找马航MH370航班过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=1500米,tanα=
在寻找马航MH370航班过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=1500米,tanα=
| ||
| 5 |
A、2400
| ||
B、2400
| ||
C、2500
| ||
D、2500
|
已知非负数a,b,c满足a+b=2,c-3a=4,设S=a2+b+c的最大值为m,最小值为n,则m-n的值为( )
| A、9 | ||
| B、8 | ||
| C、1 | ||
D、
|
分式
+
的化简结果为( )
| 1 |
| x |
| 1 |
| x(x-1) |
| A、x | ||
B、
| ||
C、
| ||
D、
|
已知sinA=
,则下列正确的是( )
| 1 |
| 2 |
A、cosA=
| ||||
B、cosA=
| ||||
| C、tanA=1 | ||||
D、tanA=
|
 如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为
如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为 如图,在矩形纸片ABCD中,AB=6,BC=8,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G,E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE 沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G,E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE 沿EF折叠,使点D落在D′处,点D′恰好与点A重合.