题目内容
17. 如图,边长为4的等边△ABC和等边△DEF互相重合,现将△ABC沿直线l向左平移m个单位,将△DEF沿直线l向右平移m个单位.
如图,边长为4的等边△ABC和等边△DEF互相重合,现将△ABC沿直线l向左平移m个单位,将△DEF沿直线l向右平移m个单位.(1)若m=1,则BE=2;
(2)当E、C是线段BF的三等分点时,m的值为1或4.
分析 (1)根据点平移的性质可得出BE=2m,代入m的值即可得出结论;
(2)分点E、C的位置不同,两种情况来考虑,根据线段间的关系结合BC=4即可得出关于m的一元一次方程,解方程即可得出结论.
解答 解:(1)∵点B向左平移m个单位,点E向右平移m个单位,
∴BE=2m,
∵m=1,
∴BE=2m=2.
故答案为:2.
(2)E、C是线段BF的三等分点分两种情况:
①点E在点C的左边时,如图1所示.
∵E、C是线段BF的三等分点,
∴BE=EC=CF,
∵BC=4,BE=2m,
∴2m=4÷2,解得:m=1;
②点E在点C的右边时,如图2所示.
∵E、C是线段BF的三等分点,
∴BC=CE=EF,
∵BC=4,BE=2m,
∴2m=4×2,解得:m=4.
综上可知:当E、C是线段BF的三等分点时,m的值为1或4.
故答案为:1或4.
点评 本题考查了等边三角形的性质以及平移的性质,解题的关键是:(1)找出BE=2m;(2)分两种情况考虑.本题属于中档题,难度不大,解决(2)时,很多同学往往忘记考虑到第二种情况,造成失分,故应在日常学习中多做些分类讨论(分段)的练习题.

练习册系列答案
相关题目
7.在平面直角坐标中,线段A′B′是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A′(3,1),点B的对应点B′(4,0),则点B的坐标为( )
| A. | (-1,-1) | B. | (-1,0) | C. | (-2,-1) | D. | (-3,0) |
5. 如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
 如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )| A. | 50π | B. | 50 | C. | 500π | D. | 500 |
 如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为12cm.
如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为12cm. 如图,在每个小正方形边长均为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长均为1的方格纸中,△ABC的顶点都在方格纸格点上.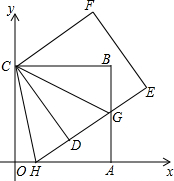 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG. 如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.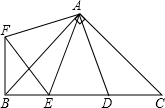 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE2+DC2=DE2;④BE+DC=DE,其中正确的是①②③(只填序号)
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE2+DC2=DE2;④BE+DC=DE,其中正确的是①②③(只填序号)