Question

1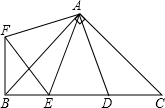．如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②△ABC的面积等于四边形AFBD的面积；③BE²+DC²=DE²；④BE+DC=DE，其中正确的是①②③（只填序号）

Answer 1

分析 首先根据旋转的性质得到∠FAD=90°，DC=BF，∠FBE=90°，AD=AF，而∠DAE=45°，即可利用SAS判定△AED≌△AEF；由旋转的性质易得△AFB≌△ADC，又由S_△ABC=S_△ABD+S_△ADC，S_{四边形AFBD}=S_△ABD+S_△AFB，即可判定△ABC的面积等于四边形AFBD的面积；由在Rt△BEF中，BE²+BF²=EF²，即可得BE²+DC²=DE²．

解答 解：∵△ADC绕点A顺时针90°旋转后，得到△AFB，
∴∠FAD=90°，DC=BF，∠FBE=90°，AD=AF，
∵∠DAE=45°，
∴∠EAF=90°-45°=45°，
在△AED和△AEF中，
$\left\{\begin{array}{l}{AD=AF}\\{∠DAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△AED≌△AEF（SAS）；故①正确；
∵将△ADC绕点A顺时针旋转90°后，得到△AFB，
∴△AFB≌△ADC，
∴S_△AFB=S_△ADC，
∵S_△ABC=S_△ABD+S_△ADC，S_{四边形AFBD}=S_△ABD+S_△AFB，
∴△ABC的面积等于四边形AFBD的面积；故②正确；
∵△AED≌△AEF，
∴EF=ED，
在Rt△BEF中，BE²+BF²=EF²，
∴BE²+DC²=DE²．故③正确；④错误．
故答案为：①②③．

点评 此题属于三角形的综合题．考查了旋转的性质、全等三角形的判定与性质以及勾股定理等知识．注意掌握旋转前后图形的对应关系是解此题的关键．