Question

9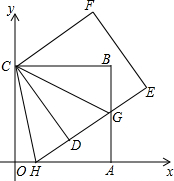．如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连结CH、CG．
（1）求证：CG平分∠DCB；
（2）在正方形ABCO绕点C逆时针旋转的过程中，求线段HG、OH、BG之间的数量关系；
（3）连接BD、DA、AE、EB，在旋转过程中，四边形AEBD能否成为矩形？
若能，试求出直线DE的解析式；若不能，请说明理由．

Answer 1

分析 （1）根据旋转和正方形的性质可得出CD=CB，∠CDG=∠CBG=90，根据全等直角三角形的判定定理（HL）即可证出Rt△CDG≌Rt△CBG，即∠DCG=∠BCG，由此即可得出CG平分∠DCB；
（2）由（1）的Rt△CDG≌Rt△CBG可得出BG=DG，根据全等直角三角形的判定定理（HL）即可证出Rt△CHO≌Rt△CHD，即OH=HD，再根据线段间的关系即可得出HG=HD+DG=OH+BG；
（3）根据（2）的结论即可找出当G点为AB中点时，四边形AEBD为矩形，再根据正方形的性质以及点B的坐标可得出点G的坐标，设H点的坐标为（x，0），由此可得出HO=x，根据勾股定理即可求出x的值，即可得出点H的坐标，结合点H、G的坐标利用待定系数法即可求出直线DE的解析式．

解答 解：（1）证明：∵正方形ABCO绕点C旋转得到正方形CDEF，
∴CD=CB，∠CDG=∠CBG=90°，
在Rt△CDG和Rt△CBG中，$\left\{\begin{array}{l}CG=CG\\ CD=CB\end{array}\right.$，
∴Rt△CDG≌Rt△CBG（HL）．
∴∠DCG=∠BCG，
即CG平分∠DCB．
（2）由（1）证得：Rt△CDG≌Rt△CBG，
∴BG=DG，
在Rt△CHO和Rt△CHD中，$\left\{\begin{array}{l}CH=CH\\ CO=CD\end{array}\right.$，
∴Rt△CHO≌Rt△CHD（HL），
∴OH=HD，
∴HG=HD+DG=OH+BG．
（3）假设四边形AEBD可为矩形．
当G点为AB中点时，四边形AEBD为矩形，如图所示．
∵G点为AB中点，
∴$BG=GA=\frac{1}{2}AB$，
由（2）证得：BG=DG，则$BG=GA=DG=\frac{1}{2}AB=\frac{1}{2}DE=GE$，
又AB=DE，
∴四边形AEBD为矩形．
∴AG=EG=BG=DG．
∵$AG=\frac{1}{2}AB=3$，
∴G点的坐标为（6，3）．
设H点的坐标为（x，0），则HO=x，
∴HD=x，DG=3，
∵OH=DH，BG=DG，
在Rt△HGA中，HG=x+3，GA=3，HA=6-x，
由勾股定理得：（x+3）²=3²+（6-x）²，解得：x=2，
∴H点的坐标为（2，0）．
设直线DE的解析式为：y=kx+b（k≠0），
将点H（2，0）、G（6，3）代入y=kx+b中，
得：$\left\{\begin{array}{l}2k+b=0\\ 6k+b=3\end{array}\right.$，解得：$\left\{\begin{array}{l}k=\frac{3}{4}\\ b=-\frac{3}{2}\end{array}\right.$，
∴直线DE的解析式为：$y=\frac{3}{4}x-\frac{3}{2}$．
故四边形AEBD能为矩形，此时直线DE的解析式为：$y=\frac{3}{4}x-\frac{3}{2}$．

点评 本题考查了矩形的性质、旋转的性质、全等三角形的判定及性质、待定系数法求函数解析式以及勾股定理，解题的关键是：（1）证出Rt△CDG≌Rt△CBG；（2）找出BG=DG、OH=HD；（3）求出点H、G的坐标．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边和角是关键．