题目内容
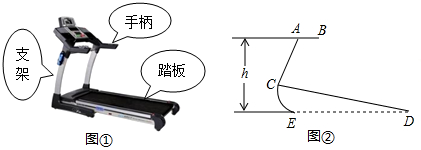
图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

考点:解直角三角形的应用
专题:几何图形问题
分析:过C点作FG⊥AB于F,交DE于G.在Rt△ACF中,根据三角函数可求CF,在Rt△CDG中,根据三角函数可求CG,再根据FG=FC+CG即可求解.
解答: 解:过C点作FG⊥AB于F,交DE于G.
解:过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+12°-80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=AC•sin∠CAF≈0.744m,
在Rt△CDG中,CG=CD•sin∠CDE≈0.336m,
∴FG=FC+CG≈1.1m.
故跑步机手柄的一端A的高度约为1.1m.
 解:过C点作FG⊥AB于F,交DE于G.
解:过C点作FG⊥AB于F,交DE于G.∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+12°-80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=AC•sin∠CAF≈0.744m,
在Rt△CDG中,CG=CD•sin∠CDE≈0.336m,
∴FG=FC+CG≈1.1m.
故跑步机手柄的一端A的高度约为1.1m.
点评:此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目


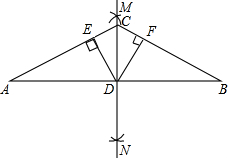 如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F.
如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F. 某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为
某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为