题目内容
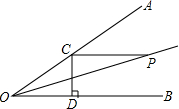 如图,∠AOB=30°,P是∠AOB的平分线上一点,PC∥OB,交OA于C,CD⊥OB于D.若PC=3,则CD的长为
如图,∠AOB=30°,P是∠AOB的平分线上一点,PC∥OB,交OA于C,CD⊥OB于D.若PC=3,则CD的长为考点:含30度角的直角三角形,等腰三角形的判定与性质
专题:
分析:根据角平分线的定义可得∠AOP=∠BOP,再根据两直线平行,内错角相等可得∠OPC=∠BOP,然后求出∠AOP=∠OPC,再根据等角对等边可得OC=PC,然后利用直角三角形30°角所对的直角边等于斜边的一半可得CD=
OC.
| 1 |
| 2 |
解答:解:∵OP是∠AOB的平分线,
∴∠AOP=∠BOP,
∵PC∥OB,
∴∠OPC=∠BOP,
∴∠AOP=∠OPC,
∴OC=PC=3,
∵∠AOB=30°,CD⊥OB,
∴CD=
OC=
.
故答案为:
.
∴∠AOP=∠BOP,
∵PC∥OB,
∴∠OPC=∠BOP,
∴∠AOP=∠OPC,
∴OC=PC=3,
∵∠AOB=30°,CD⊥OB,
∴CD=
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了平行线是性质,等腰三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
一个等腰三角形的两边长分别是3和7,则它的周长为( )
| A、17 | B、15 |
| C、13 | D、13或17 |
 如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是
如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是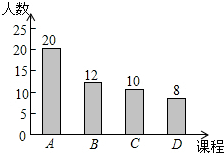 某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有
某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有
