题目内容
求证：对任意整数n，（n2）2+6n3-n2-6n能被24整除．
考点：因式分解的应用
专题：证明题
分析：利用提取公因式法对（n2）2+6n3-n2-6n进行因式分解，将其转化为n（n+6）（n+1）（n+2）的形式，因为2n，n+1，n+2是连续整数，则易推知（n2）2+6n3-n2-6n能被24整除．
解答：证明：n4+6n3-n2-6n=n3（n+6）-n（n+6）=n（n+6）（n+1）（n+2），
∵n，n+1，n+2是连续整数，
∴其中必有一个是2的倍数、一个是3的倍数，一个是4的倍数，
∴n（n+6）（n+1）（n+2）能被24整除，
即（n2）2+6n3-n2-6n能被24整除．
∵n，n+1，n+2是连续整数，
∴其中必有一个是2的倍数、一个是3的倍数，一个是4的倍数，
∴n（n+6）（n+1）（n+2）能被24整除，
即（n2）2+6n3-n2-6n能被24整除．
点评：主要考查了分解因式的实际运用，解此类题目的关键是把（n2）2+6n3-n2-6n转化为n（n+6）（n+1）（n+2）的形式．
练习册系列答案
相关题目
如图，梯形ABCD中，对角线AC、BD交于O，△AOB面积为a2，△DOC面积为b2，则梯形ABCD的面积是
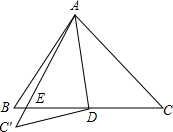如图所示，AD是△ABC的中线，现把△ADC沿AD翻折，得△ADC′，AC′与DB交于点E，则△ABE和△C′ED的面积之比为
如图，在正方形ABCD中，AB=2cm，对角线AC、BD交于点O，点E以一定的速度从A向B移动，点F以相同的速度从B向C移动，连结OE、OF、EF．