题目内容
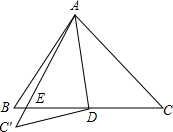如图所示，AD是△ABC的中线，现把△ADC沿AD翻折，得△ADC′，AC′与DB交于点E，则△ABE和△C′ED的面积之比为考点：翻折变换（折叠问题）
专题：
分析：根据三角形的中线把三角形分成两个面积相等的三角形可得S△ABD=S△ACD，根据翻折的不变性可得S△ACD=S△AC′D，再求出S△ABE=S△C′ED，从而得解．
解答：解：∵AD是△ABC的中线，
∴S△ABD=S△ACD，
∵△ADC沿AD翻折得△ADC′，
∴S△ACD=S△AC′D，
∵S△ABE=S△ABD-S△ADE，
S△C′ED=S△AC′D-S△ADE，
∴S△ABE=S△C′ED，
∴△ABE和△C′ED的面积之比为1：1．
故答案为：1：1．
∴S△ABD=S△ACD，
∵△ADC沿AD翻折得△ADC′，
∴S△ACD=S△AC′D，
∵S△ABE=S△ABD-S△ADE，
S△C′ED=S△AC′D-S△ADE，
∴S△ABE=S△C′ED，
∴△ABE和△C′ED的面积之比为1：1．
故答案为：1：1．
点评：本题考查了翻折的性质，主要利用了三角形的中线把三角形分成两个面积相等的三角形的性质，需熟记．
练习册系列答案
相关题目
如图，正方形ABCD的边长为6，E为BC上一点，CE=2BE，将△ABE沿AE折叠得到△AFE，连接DF，则线段DF的长度是多少？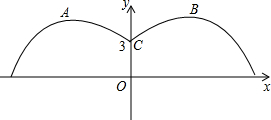
如图，一盆君子兰花的两片绿叶是形状相同的抛物线，它们的交接处距花土面3cm，两片绿叶最高点之间的距离是12cm，最高点到花土面的距离是4.2m，分别求出左、右两边抛物线的解析式．
如图所示，已知DF⊥AC，BE⊥AC，CD=AB，AF=CE．求证：DC∥AB．
下列方程是一元二次方程的是（ ）
A、
| ||
| B、x2+2x-y=3 | ||
| C、ax2-bx=5（a和b为常数） | ||
| D、m2-2m=3 |
计算-5+6的结果是（ ）
| A、-1 | B、1 | C、-5 | D、-6 |