题目内容
如图，梯形ABCD中，对角线AC、BD交于O，△AOB面积为a2，△DOC面积为b2，则梯形ABCD的面积是考点：梯形,相似三角形的判定与性质
专题：
分析：先证明△COD∽△AOB，得到CO和AO的关系，又因为S△ABC=S△ABD，所以S△ABC-S△AOB=S△ABD-S△AOB，即S△BOC=S△AOD，进而得到a，b和S的关系．
解答：解：∵AB∥CD，
∴△COD∽△AOB，
∴
=(
)2=
，
∴又∵S△ABC=S△ABD，
∴
=
=
，
∵S△ABC=S△ABD，
∴S△ABC-S△AOB=S△ABD-S△AOB，
即S△BOC=S△AOD，
∵
=
=
，
∴S△AOD=
•S△COD=
•a2=ab，
∴S△BOC=ab，
∴S=S△COD+S△AOD+S△BOC+S△AOB=a2+ab+ab+b2=（a+b）2．
∴△COD∽△AOB，
∴
| S△COD |
| S△AOB |
| CO |
| AO |
| a2 |
| b2 |
∴又∵S△ABC=S△ABD，
∴
| CO |
| AO |
|
| a |
| b |
∵S△ABC=S△ABD，
∴S△ABC-S△AOB=S△ABD-S△AOB，
即S△BOC=S△AOD，
∵
| S△AOD |
| S△COD |
| AO |
| CO |
| b |
| a |
∴S△AOD=
| b |
| a |
| b |
| a |
∴S△BOC=ab，
∴S=S△COD+S△AOD+S△BOC+S△AOB=a2+ab+ab+b2=（a+b）2．
点评：此题考查了相似三角形的判定和性质、梯形的性质，关键是灵活利用相似三角形的性质进行转化和求解．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
设x是有理数，那么下列各式中一定表示正数的是（ ）
| A、2014x |
| B、x+2014 |
| C、|2014x| |
| D、|x|+2014 |
如图，正方形ABCD的边长为6，E为BC上一点，CE=2BE，将△ABE沿AE折叠得到△AFE，连接DF，则线段DF的长度是多少？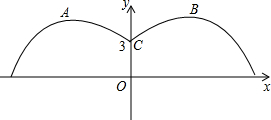
如图，一盆君子兰花的两片绿叶是形状相同的抛物线，它们的交接处距花土面3cm，两片绿叶最高点之间的距离是12cm，最高点到花土面的距离是4.2m，分别求出左、右两边抛物线的解析式．