题目内容
17.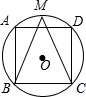 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM.
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM.(1)求证:BM=CM;
(2)当⊙O的半径为2时,求$\widehat{BM}$的长.
分析 (1)根据圆心距、弦、弧之间的关系定理解答即可;
(2)根据弧长公式计算.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∵M为$\widehat{AD}$中点,
∴$\widehat{AM}$=$\widehat{DM}$,
∴$\widehat{AB}$+$\widehat{AM}$=$\widehat{CD}$+$\widehat{DM}$,即$\widehat{BM}$=$\widehat{CM}$,
∴BM=CM;
(2)解:∵⊙O的半径为2,
∴⊙O的周长为4π,
∵$\widehat{AM}$=$\widehat{DM}$=$\frac{1}{2}$$\widehat{AD}$=$\frac{1}{2}$$\widehat{AB}$,
∴$\widehat{BM}$=$\widehat{AB}$+$\widehat{AM}$=$\frac{3}{2}\widehat{AB}$,
∴$\widehat{BM}$的长=$\frac{3}{2}$×$\frac{1}{4}$×4π=$\frac{3}{8}$×4π=$\frac{3}{2}$π.
点评 本题考查的是正方形的性质、弧长的计算、圆心距、弦、弧之间的关系,掌握弧长的计算公式、圆心距、弦、弧之间的关系定理是解题的关键.

练习册系列答案
相关题目
8.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
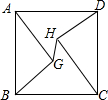

| A. | $\frac{8\sqrt{3}}{5}$ | B. | 2$\sqrt{2}$ | C. | $\frac{14}{5}$ | D. | 10-5$\sqrt{2}$ |
5.下列说法中,正确的是( )
| A. | 不可能事件发生的概率为0 | |
| B. | 随机事件发生的概率为$\frac{1}{2}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |
9.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
6.一个不透明布袋里装有1个白球、2个黑球、3个红球,它们除颜色外均相同.从中任意摸出一个球,则是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.2016年第一季度,我市“蓝天白云、繁星闪烁”天数持续增加,获得山东省环境空气质量生态补偿资金408万元,408万用科学记数法表示正确的是( )
| A. | 408×104 | B. | 4.08×104 | C. | 4.08×105 | D. | 4.08×106 |