题目内容
12.已知四个点的坐标分别是(-1,1),(2,2),($\frac{2}{3}$,$\frac{3}{2}$),(-5,-$\frac{1}{5}$),从中随机选取一个点,在反比例函数y=$\frac{1}{x}$图象上的概率是$\frac{1}{2}$.分析 先判断四个点的坐标是否在反比例函数y=$\frac{1}{x}$图象上,再让在反比例函数y=$\frac{1}{x}$图象上点的个数除以点的总数即为在反比例函数y=$\frac{1}{x}$图象上的概率,依此即可求解.
解答 解:∵-1×1=-1,
2×2=4,
$\frac{2}{3}$×$\frac{3}{2}$=1,
(-5)×(-$\frac{1}{5}$)=1,
∴2个点的坐标在反比例函数y=$\frac{1}{x}$图象上,
∴在反比例函数y=$\frac{1}{x}$图象上的概率是2÷4=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
3.人类的遗传物质是DNA,DNA是一个很长的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )
| A. | 3×107 | B. | 30×106 | C. | 0.3×107 | D. | 0.3×108 |
20.下列实数中的无理数是( )
| A. | 0.7 | B. | $\frac{1}{2}$ | C. | π | D. | -8 |
7.平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )
| A. | (-2,1) | B. | (-2,-1) | C. | (-1,-2) | D. | (-1,2) |
4. 若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
 若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )| A. | a<0 | B. | ab<0 | C. | a<b | D. | a,b互为倒数 |
1.6的相反数是( )
| A. | -6 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | 6 |
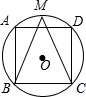 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM.
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM.