题目内容
9.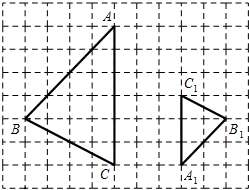 如图,在8×11网格图中,△ABC与△A1B1C1是位似图形.
如图,在8×11网格图中,△ABC与△A1B1C1是位似图形.(1)若在网格上建立平面直角坐标系,使得点A的坐标为(-1,6),点C1的坐标为(2,3),则点B的坐标为(-5,2);
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为 1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为(1,2),计算四边形ABCP的周长为6$\sqrt{2}$+4$\sqrt{5}$.
分析 (1)利用点A和C1的坐标画出直角坐标系,然后写出B点坐标;
(2)利用网格特点,根据位似的性质取AB的中点B2和AC的中点C2,则△AB2C2和△ABC位似,且位似比为 1:2;
(3)连结AA1、CC1、BB1,它们相交于点P,再写出P点坐标,然后利用勾股定理计算AB、BC、PC和AP的长,从而可得到四边形ABCP的周长.
解答  解:(1)如图,点B的坐标为(-5,2);
解:(1)如图,点B的坐标为(-5,2);
(2)如图,△AB2C2△为所作;
(3)如图,点P为所作,P点坐标为(1,2),
AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,PC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,AP=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$
所以四边形ABCP的周长=4$\sqrt{2}$+2$\sqrt{5}$+2$\sqrt{2}$+2$\sqrt{5}$=6$\sqrt{2}$+4$\sqrt{5}$.
故答案为(-5,2),(1,2),6$\sqrt{2}$+4$\sqrt{5}$.
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;然后根据位似比,确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目
19.已知a-b+c=0,则一元二次方程ax2+bx+c=0(a≠0)必有一个根是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -1 |
17.在光下,某建筑物的影长为24米,同时旁边3米长的标杆的影长是2米,则该建筑物的高度为( )
| A. | 16米 | B. | 18米 | C. | 32米 | D. | 36米 |
1.一正多边形外角为90°,则它的边心距与半径之比为( )
| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:3 |
19.四舍五入得到的近似数0.03050的有效数字有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
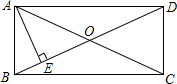 如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数.
如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数.