题目内容
4．两个相似三角形对应边上的中线之比为2：3，则这两个三角形的面积之比为4：9．分析 根据相似三角形对应边上的中线之比等于相似比，相似三角形面积的比等于相似比的平方进行解答即可．
解答 解：∵两个相似三角形对应边上的中线之比为2：3，
∴两个相似三角形相似比为2：3，
∴两个相似三角形的面积之比为4：9，
故答案为：4：9．
点评 本题考查对相似三角形性质：相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
练习册系列答案
备战中考寒假系列答案
相关题目
14．
如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）
如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）| A． | 3 | B． | 3.5 | C． | 5 | D． | 5.5 |
15．某地遭遇旱灾，约10万人的生活受到严重影响，现调拨一批粮食救济灾区人民的生活，若这批粮食可供灾区人民生活20天，平均每人每天需0.5千克，则这批救济粮约为（ ）
| A． | 1.0×106千克 | B． | 1.0×105千克 | C． | 1.0×107千克 | D． | 1.0×108千克 |
19．若两个相似三角形的面积之比为4：9，则它们对应角的平分线之比为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{6}}{2}$ |
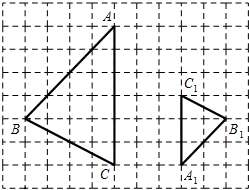如图，在8×11网格图中，△ABC与△A1B1C1是位似图形．
已知实数a，b在数轴上位置如图所示，化简$|a|-\sqrt{b^2}+\sqrt{{{（{a-b}）}^2}}-\sqrt{4{a^2}}$．