题目内容
1．一正多边形外角为90°，则它的边心距与半径之比为（ ）| A． | 1：2 | B． | 1：$\sqrt{2}$ | C． | 1：$\sqrt{3}$ | D． | 1：3 |
分析 利用多边形的外角和是360度，判断该多边形的形状，根据正方形的性质求出它的边心距与半径之比．
解答 解：∵多边形的外角和是360度，正多边形的一个外角为90°，
∴正边形的边数是360÷90=4，
∴这个多边形是正方形，
∵∠AOB=90°，OA=OB，
∴∠OAC=45°，
∴它的边心距与半径之比为1：$\sqrt{2}$．
故选：B．
点评 本题考查的是正多边形和圆的一个计算，掌握多边形的外角和是360度和正多边形的每个外角相等是解题的关键．
练习册系列答案
相关题目
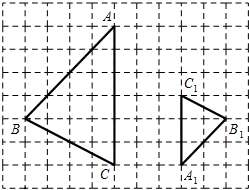如图，在8×11网格图中，△ABC与△A1B1C1是位似图形．
已知实数a，b在数轴上位置如图所示，化简$|a|-\sqrt{b^2}+\sqrt{{{（{a-b}）}^2}}-\sqrt{4{a^2}}$．