题目内容
19．已知a-b+c=0，则一元二次方程ax2+bx+c=0（a≠0）必有一个根是（ ）| A． | 1 | B． | -2 | C． | 0 | D． | -1 |
分析 一元二次方程ax2+bx+c=0中几个特殊值的特殊形式：x=1时，a+b+c=0；x=-1时，a-b+c=0．只需把x=-1代入一元二次方程ax2+bx+c=0中验证a-b+c=0即可．
解答 解：把x=-1代入一元二次方程ax2+bx+c=0中得，a-b+c=0，
所以当a-b+c=0，且a≠0，则一元二次方程ax2+bx+c=0必有一个定根是-1．
故选：D．
点评 本题考查的是一元二次方程的根，即方程的解的定义．解该题的关键是要掌握一元二次方程ax2+bx+c=0中几个特殊值的特殊形式：x=1时，a+b+c=0；x=-1时，a-b+c=0．
练习册系列答案
教材全解字词句篇系列答案
相关题目
9．已知点M（2m-1，3m+5）到y轴的距离是它到x轴距离的2倍，则m的值为（ ）
| A． | -$\frac{11}{4}$ | B． | 7 | C． | 7或-$\frac{3}{7}$ | D． | -$\frac{11}{4}$或-$\frac{9}{8}$ |
10．下列各数中0、21、-$\frac{2}{5}$、-25%、$\frac{π}{3}$、-|-2-3|、0.65（65循环）、3.14-π、-$\frac{22}{7}$整数的个数为x，非负数的个数是y，分数的个数是z，则x+y+z的值为（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 以上都不对 |
7．数轴上表示2和5的点分别为A和B，点B关于点A的对称点是点C，则点C所表示的数是（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
14．
如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）
如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）| A． | 3 | B． | 3.5 | C． | 5 | D． | 5.5 |
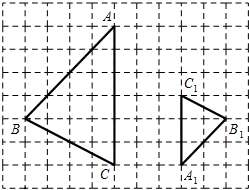如图，在8×11网格图中，△ABC与△A1B1C1是位似图形．