题目内容
20.已知方程组$\left\{\begin{array}{l}2x+y=2-m\\ x+2y=2\end{array}\right.$的解x,y满足x>0,y>0,则m的取值范围是-2<m<1.分析 把m看做已知数表示出方程组的解,根据x与y都大于0,求出m的范围即可.
解答 解:$\left\{\begin{array}{l}{2x+y=2-m①}\\{x+2y=2②}\end{array}\right.$,
①×2-②得:3x=2-2m,即x=$\frac{2-2m}{3}$,
②×2-①得:3y=2+m,即y=$\frac{2+m}{3}$,
根据x>0,y>0,得$\left\{\begin{array}{l}{\frac{2-2m}{3}>0}\\{\frac{2+m}{3}>0}\end{array}\right.$,
解得:-2<m<1,
故答案为:-2<m<1
点评 此题考查了二元一次方程组的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列各数中0、21、-$\frac{2}{5}$、-25%、$\frac{π}{3}$、-|-2-3|、0.65(65循环)、3.14-π、-$\frac{22}{7}$整数的个数为x,非负数的个数是y,分数的个数是z,则x+y+z的值为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 以上都不对 |
15.某地遭遇旱灾,约10万人的生活受到严重影响,现调拨一批粮食救济灾区人民的生活,若这批粮食可供灾区人民生活20天,平均每人每天需0.5千克,则这批救济粮约为( )
| A. | 1.0×106千克 | B. | 1.0×105千克 | C. | 1.0×107千克 | D. | 1.0×108千克 |
5.如果|a+1|=3,则a的值为( )
| A. | 1 | B. | 3 | C. | 2或-4 | D. | 2或-3 |
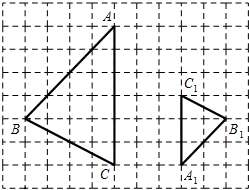 如图,在8×11网格图中,△ABC与△A1B1C1是位似图形.
如图,在8×11网格图中,△ABC与△A1B1C1是位似图形.