题目内容
 定义:如果二次函数y=ax2+bx+c的最小值大于0,我们就说这个二次函数的值恒大于0.
定义:如果二次函数y=ax2+bx+c的最小值大于0,我们就说这个二次函数的值恒大于0.(1)如图所示,如果二次函数的值恒大于0,那么它图象上的点都在x轴上方.根据图象可知:a
(2)试判断二次函数y=2x2-2x+1的值是否恒大于0;
(3)类似的,可以定义二次函数y=ax2+bx+c的值恒小于0:
(4)如果二次函数y=x2-2x+k的值恒大于0,求k的取值范围.
考点:抛物线与x轴的交点,二次函数的最值
专题:
分析:(1)根据抛物线的开口方向和抛物线与x轴交点的个数进行填空;
(2)根据根的判别式的符号进行推断;
(3)根据材料中的“定义”填空;
(4)由“定义”得到关于k的不等式△=4-4k<0,通过解不等式来求k的取值范围.
(2)根据根的判别式的符号进行推断;
(3)根据材料中的“定义”填空;
(4)由“定义”得到关于k的不等式△=4-4k<0,通过解不等式来求k的取值范围.
解答: 解:(1)如图所示,如果二次函数的值恒大于0,那么它图象上的点都在x轴上方.根据图象可知:a>0,b2-4ac<0.
解:(1)如图所示,如果二次函数的值恒大于0,那么它图象上的点都在x轴上方.根据图象可知:a>0,b2-4ac<0.
故答案是:>;<;
(2)y=2x2-2x+1=2(x-
)2+
,
∵2>0,所以图象开口向上,b2-4ac=-4<0,图象与x轴没有公共点,所以函数的值恒大于0;
(3)类似的,可以定义二次函数y=ax2+bx+c的值恒小于0:如果二次函数y=ax2+bx+c的最大值小于0,我们就说这个二次函数的值恒小于0.如果二次函数的值恒小于0,那么a<0,b2-4ac<0.
故答案是:如果二次函数y=ax2+bx+c的最大值小于0,我们就说这个二次函数的值恒小于0;<;<;
(4)∵二次函数y=x2-2x+k的值恒大于0,
∴△=4-4k<0.
解得 k>1.
 解:(1)如图所示,如果二次函数的值恒大于0,那么它图象上的点都在x轴上方.根据图象可知:a>0,b2-4ac<0.
解:(1)如图所示,如果二次函数的值恒大于0,那么它图象上的点都在x轴上方.根据图象可知:a>0,b2-4ac<0.故答案是:>;<;
(2)y=2x2-2x+1=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
∵2>0,所以图象开口向上,b2-4ac=-4<0,图象与x轴没有公共点,所以函数的值恒大于0;
(3)类似的,可以定义二次函数y=ax2+bx+c的值恒小于0:如果二次函数y=ax2+bx+c的最大值小于0,我们就说这个二次函数的值恒小于0.如果二次函数的值恒小于0,那么a<0,b2-4ac<0.
故答案是:如果二次函数y=ax2+bx+c的最大值小于0,我们就说这个二次函数的值恒小于0;<;<;
(4)∵二次函数y=x2-2x+k的值恒大于0,
∴△=4-4k<0.
解得 k>1.
点评:本题考查了抛物线与x轴的交点和二次函数的最值,解答该类题目,运用“数形结合”的数学思想,可以使问题变得直观化,降低解题的难度.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,仿照以上推理,计算出1+5+52+53+…+52013的值为( )
| A、52014-1 | ||
| B、52015-1 | ||
C、
| ||
D、
|
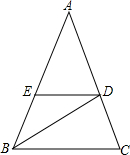 在△ABC中,∠ABC=∠C=2∠A,BD是∠ABC的平分线,DE∥BC,则图中等腰三角形的个数是( )
在△ABC中,∠ABC=∠C=2∠A,BD是∠ABC的平分线,DE∥BC,则图中等腰三角形的个数是( )| A、5 | B、4 | C、3 | D、2 |
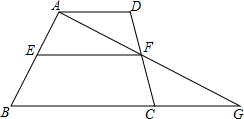 如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且
如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且