题目内容
9.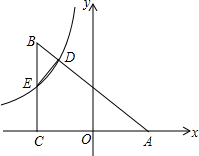 如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.
如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.
分析 根据题意表示出E与D坐标,由AC与BC的长表示出C,B,A的坐标,设直线AB解析式为y=kx+m,把A与B坐标代入表示出k与m,进而表示出直线AB解析式,由三角形BDE与三角形BCA相似,得到DE与AB垂直,过点D作x轴的垂线,过点E作y轴的垂线,两线交于点H,如图所示,得到三角形EHD与三角形BCA相似,表示出HE与HD的关系式,即可得出a与b的关系式.
解答 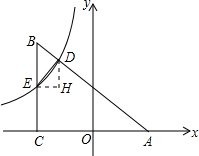 解:∵∠BCA=90°,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E,点E、D的横坐标分别为a、b,
解:∵∠BCA=90°,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E,点E、D的横坐标分别为a、b,
∴E(a,-$\frac{4}{3a}$),D(b,-$\frac{4}{3b}$),
∵AC=4,BC=3,
∴C(a,0),B(a,3),A(4+a,0),
设直线AB的解析式为y=kx+m,
∴$\left\{\begin{array}{l}{(4+a)k+m=0}\\{ak+m=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{m=3+\frac{3}{4}a}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{3}{4}$x+3+$\frac{3}{4}$a,
又∵△BDE∽△BCA,
∴∠BDE=∠BCA=90°,
∴AB⊥DE,
过点D作x轴的垂线,过点E作y轴的垂线,两线交于点H,如图所示,
∴△EHD∽△BCA,
∴HE=$\frac{3}{4}$HD,即b-a=$\frac{3}{4}$($\frac{4}{3a}$-$\frac{4}{3b}$),
∴b=$\frac{1}{a}$.
故答案为:b=$\frac{1}{a}$
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定一次函数解析式,坐标与图形性质,相似三角形的判定与性质,以及反比例函数的性质,熟练掌握待定系数法是解本题的关键.

 名校课堂系列答案
名校课堂系列答案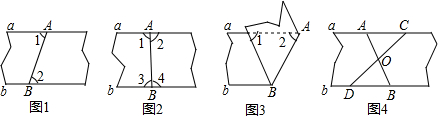
| A. | 如图1,展开后测得∠1=∠2 | |
| B. | 如图2,展开后测得∠1=∠2且∠3=∠4 | |
| C. | 如图3,测得∠1=∠2 | |
| D. | 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD |
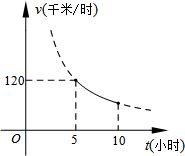 一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.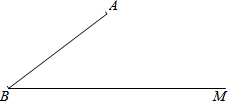 如图,已知∠ABM=37°,AB=20,C是射线BM上一点.
如图,已知∠ABM=37°,AB=20,C是射线BM上一点.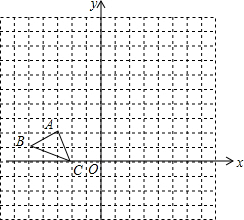 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).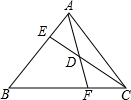 已知D为AF的中点,BF=2FC,求AE:BE的值.
已知D为AF的中点,BF=2FC,求AE:BE的值.