题目内容
1.取一张正方形纸片,如图①所示,折叠一个角,设顶点A落在A′的位置,折痕为CD,再折叠另一个角,如图②所示,使BD沿DA′方向落下,折痕为DE,试判断DE、DC的位置关系,并说明理由.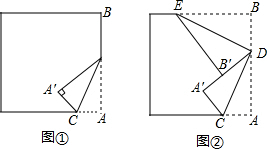
分析 由翻折的性质可知∠ADC=∠A′DC,∠BDE=∠B′DE,从而可得到∠EDC=90°.
解答 解:ED⊥CD.
理由:∵由翻折的性质可知:∠ADC=∠A′DC,∠BDE=∠B′DE,
∴∠EDA′=$\frac{1}{2}∠BDB′$,∠A′DC=$\frac{1}{2}∠$A′DA.
∴∠EDC=$\frac{1}{2}(∠BDB′+∠B′DA)$=$\frac{1}{2}×180°$=90°.
∴ED⊥DC.
点评 本题主要考查的是翻折的性质,掌握翻折的性质是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.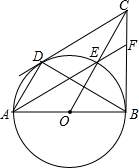 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
10.下列运算正确的是( )
| A. | 2x•3x2=6x2 | B. | x6÷x2=x3 | C. | (x-y)2=x2-y2 | D. | -x(x-y)=-x2+xy |