Question

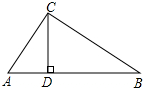如图，△ABC中，∠ACB=90°，CD是高，若AB=13cm，AC=5cm，求CD的长．

Answer 1

考点：勾股定理

专题：计算题

分析：在直角三角形ABC中，由AB与AC的长，利用勾股定理求出BC的长，再利用面积法求出CD的长即可．

解答：解：在Rt△ABC中，AB=13cm，AC=5cm，
根据勾股定理得：BC=

132-52

=12cm，
∵S_△ABC=

1

2

AC•BC=

1

2

AB•CD，即AC•BC=AB•CD，
∴5×12=13CD，
解得：CD=

60

13

cm．

点评：此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．