Question

11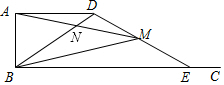．如图，已知AB=2，AD=4，∠DAB=90°，AD∥BC．E是射线BC上的动点（点E与点B不重合），M是线段DE的中点，连结BD，交线段AM于点N，如果以A、N、D为顶点的三角形与△BME相似，则线段BE的长为（　　）

• A． 3
• B． 6
• C． 3或8
• D． 2或8

Answer 1

分析 因为如果三角形ADN和BME相似，一定不相等的角是∠ADN和∠MBE，因为AD∥BC，如果两角相等，那么M与D重合，显然不合题意，故应分两种情况进行讨论．

解答 解：因为如果三角形ADN和BME相似，一定不相等的角是∠ADN和∠MBE，因为AD∥BC，如果两角相等，那么M与D重合，显然不合题意，故应分两种情况进行讨论．
①如图1，当∠ADN=∠BEM时，那么∠ADB=∠BEM，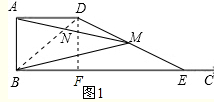
作DF⊥BE，垂足为F，
tan∠ADB=tan∠BEM．
AB：AD=DF：FE=AB：（BE-AD）．
即2：4=2：（x-4）．
解得x=8．
即BE=8．
②如图2，当∠ADB=∠BME
而∠ADB=∠DBE，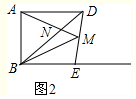
∴∠DBE=∠BME，
∵∠E是公共角，
∴△BED∽△MEB，
∴$\frac{DE}{BE}$=$\frac{BE}{EM}$，
BE²=DE•EM，
∴BE²=$\frac{1}{2}$[2²+（x-4）²]，
∴x₁=2，x₂=-10（舍去），
∴BE=2．
综上所述线段BE为8或2，
故选D．

点评 本题考查相似三角形的判定和性质、锐角三角函数、平行线的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．