题目内容
19．（1）3x（x-3）=2（x-3）（2）（2-x）2+x2=4．
分析 （1）先移项得到3x（x-3）-2（x-3）=0，然后利用因式分解法解方程；
（2）先把方程变形为（x-2）2+（x+2）（x-2）=0，然后利用因式分解法解方程．
解答 解：（1）3x（x-3）-2（x-3）=0，
（x-3）（3x-2）=0，
x-3=0或3x-2=0，
所以x1=3，x2=$\frac{2}{3}$；
（2）（x-2）2+（x+2）（x-2）=0，
（x-2）（x-2+x+2）=0，
x-2=0或x-2+x+2=0，
所以x1=2，x2=0．
点评 本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
练习册系列答案
相关题目
7．下列式子计算正确的是（ ）
| A． | （-3）-（-6）=-9 | B． | -42=-16 | C． | $\sqrt{-4}$=-2 | D． | $\sqrt{9}$=±3 |
14．如果□×3a=-3a2b，则“□”内应填的代数式是（ ）
| A． | -ab | B． | -3ab | C． | a | D． | -3a |
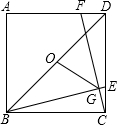如图，正方形ABCD中，E，F分别为CD，AD上一点，CE=DF，BE，CF交于点G，O为BD的中点．
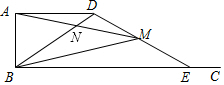如图，已知AB=2，AD=4，∠DAB=90°，AD∥BC．E是射线BC上的动点（点E与点B不重合），M是线段DE的中点，连结BD，交线段AM于点N，如果以A、N、D为顶点的三角形与△BME相似，则线段BE的长为（ ）
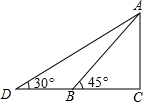如图，幼儿园为了加强安全管理，决定将园内的滑滑梯的倾角由45°降为30°，已知原滑滑梯AB的长为5m，点D，B，C在同一水平地面上．