Question

20．如图，在菱形ABCD中，∠B=120°，AD=10，AD的中点为P，AC上有动点Q，连接PQ，DQ，求PQ+DQ的最小值，并证明你的结论．

Answer 1

分析 连接BD，根据菱形的对角线平分一组对角线可得∠ABD=$\frac{1}{2}$∠ABC=60°，然后判断出△ABD是等边三角形，连接PB，根据轴对称确定最短路线问题，PB与AC的交点Q即为所求的点Q，QP+QD的最小值=PB，然后根据等边三角形的性质求出PB即可得解．

解答 ①解：如图1，连接BD、PB．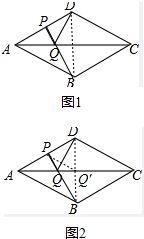
∵四边形ABCD是菱形，
∴∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×120°=60°，
∵AB=AD（菱形的邻边相等），
∴△ABD是等边三角形，
∵B、D关于对角线AC对称，图1
∴PB与AC的交点Q即为所求的点Q，PQ+QD的最小值=PB，
∵P是AD的中点，
∴PB⊥AD，
∵AD=10，
∴PB=$\frac{\sqrt{3}}{2}$×10=5$\sqrt{3}$．
②证明：如图2，在线段AC上取一点异于点Q的点Q′，连接PQ′、BQ′．
在△Q′PB中，∵Q′P+Q′B＞PB
∴Q′P+Q′B＞PQ+QB，
∵B、D关于直线AC对称，图2
∴QD=BQ，
∴Q′P+Q′B＞QP+QD
∴QP+QD最小．

点评 本题考查了轴对称确定最短路线问题、菱形的性质、等边三角形的判定与性质以及三角形的边角之间关系，熟记性质与最短路线的确定方法找出点P的位置是解题的关键．