题目内容
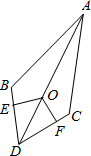 如图,已知AD为∠BAC的平分线,点O在AD上,OE⊥BD于E,OF⊥CD于F,且OE=OF,请你猜想AB与AC有什么样的数量关系?并证明.
如图,已知AD为∠BAC的平分线,点O在AD上,OE⊥BD于E,OF⊥CD于F,且OE=OF,请你猜想AB与AC有什么样的数量关系?并证明.
解:AB=AC,理由如下:
∵OE⊥BD,OF⊥CD,且OE=OF,
∴DA为∠BDC的平分线,
∴∠ADB=∠ADC,
∵AD为∠BAC的平分线,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
 ,
,
∴△ABD≌△ACD(ASA),
∴AB=AC.
分析:AB=AC,理由为:由OE⊥BD,OF⊥CD,且OE=OF,利用在角内部,到角两边距离相等的点一定在角的平分线上,得到DA为角平分线,得到一对角相等,再由AD为角平分线得到一对角相等,再由AD为公共边,利用ASA可得出三角形ABD与三角形ACD全等,由全等三角形的对应边相等可得出AB=AC,得证.
点评:此题考查了全等三角形的判定与性质,以及角平分线定义,全等三角形的判定方法有:SSS;SAS;ASA;AAS,以及HL(直角三角形判定全等的方法).
∵OE⊥BD,OF⊥CD,且OE=OF,
∴DA为∠BDC的平分线,
∴∠ADB=∠ADC,
∵AD为∠BAC的平分线,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
 ,
,∴△ABD≌△ACD(ASA),
∴AB=AC.
分析:AB=AC,理由为:由OE⊥BD,OF⊥CD,且OE=OF,利用在角内部,到角两边距离相等的点一定在角的平分线上,得到DA为角平分线,得到一对角相等,再由AD为角平分线得到一对角相等,再由AD为公共边,利用ASA可得出三角形ABD与三角形ACD全等,由全等三角形的对应边相等可得出AB=AC,得证.
点评:此题考查了全等三角形的判定与性质,以及角平分线定义,全等三角形的判定方法有:SSS;SAS;ASA;AAS,以及HL(直角三角形判定全等的方法).

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 如图,已知AD为等腰三角形ABC底边上的高,且tan∠B=
如图,已知AD为等腰三角形ABC底边上的高,且tan∠B=| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AD为∠BAC的平分线,且AD=2,AC=
如图,已知AD为∠BAC的平分线,且AD=2,AC= 17、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=
17、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD= 如图,已知AD为△ABC的角平分线,DE∥AB,如果
如图,已知AD为△ABC的角平分线,DE∥AB,如果