题目内容
如图，已知AD为∠BAC的平分线，且AD=2，AC=| 3 |
分析：根据锐角三角函数的定义可求出∠BAC的度数，再利用特殊角的三角函数值可求出AB，BC的长．
解答：解：∵AD=2，AC=
，∠C=90°
∴cos∠1=
=
，故∠1=30°
∵AD为∠BAC的平分线
∴∠BAC=∠1+∠2=30°+30°=60°
∴BC=AC•tan∠BAC=
•tan60°=
×
=3
∵△ABC是直角三角形
∴其外接圆的直径为直角三角形的斜边长，
∵AB=
=
=
=2
，
∴△ABC外接圆直径为2
．
| 3 |
∴cos∠1=
| AC |
| AD |
| ||
| 2 |
∵AD为∠BAC的平分线
∴∠BAC=∠1+∠2=30°+30°=60°
∴BC=AC•tan∠BAC=
| 3 |
| 3 |
| 3 |
∵△ABC是直角三角形
∴其外接圆的直径为直角三角形的斜边长，
∵AB=
| AC |
| cos∠BAC |
| ||
| cos60° |
| ||
|
| 3 |
∴△ABC外接圆直径为2
| 3 |
点评：此题比较简单，考查的是直角三角形的性质，解答此题是关键要明确直角三角形外接圆的直径即为三角形的斜边．
练习册系列答案
核心素养学练评系列答案
相关题目
如图，已知AD为等腰三角形ABC底边上的高，且tan∠B=| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
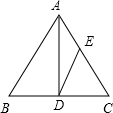
如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
17、如图，已知AD为⊙O的切线，⊙O的直径是AB=2，弦AC=1，则∠CAD=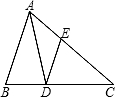
如图，已知AD为△ABC的角平分线，DE∥AB，如果