题目内容
如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：根据角平分线的定义，平行线的性质易证EA=ED，△CED∽△CAB，从而求得
的值．
| AB |
| AC |
解答：解：∵AD为△ABC的角平分线，
∴∠BAD=∠EAD，
∵DE∥AB，
∴△CED∽△CAB，∠BAD=∠EDA．
∴∠EDA=∠EAD，
∴EA=ED，
∵
=
，
∴ED：EC=2：3，
那么
=ED：EC=2：3．
故选B．
∴∠BAD=∠EAD，
∵DE∥AB，
∴△CED∽△CAB，∠BAD=∠EDA．
∴∠EDA=∠EAD，
∴EA=ED，
∵
| AE |
| EC |
| 2 |
| 3 |
∴ED：EC=2：3，
那么
| AB |
| AC |
故选B．
点评：本题主要考查了相似三角形的性质，相似三角形的对应边对应成比例．同时考查了角平分线的定义．
练习册系列答案
黄冈创优卷系列答案
相关题目
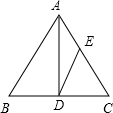如图，已知AD为等腰三角形ABC底边上的高，且tan∠B=| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知AD为∠BAC的平分线，且AD=2，AC=
17、如图，已知AD为⊙O的切线，⊙O的直径是AB=2，弦AC=1，则∠CAD=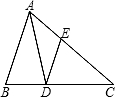
如图，已知AD为△ABC的角平分线，DE∥AB，如果