Question

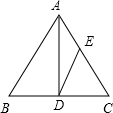如图，已知AD为等腰三角形ABC底边上的高，且tan∠B=

4

3

．AC上有一点E，满足AE：EC=2：3．那么，tan∠ADE是（　　）

• A、

  3

  5

• B、

  2

  3

• C、

  1

  2

• D、

  1

  3

Answer 1

分析：作EF∥CD，利用锐角三角函数的概念和两直线平行对应边成比例求∠ADE的正切值．

解答：解：如图．作EF∥CD交AD于F点．
∵tan∠B=tan∠C=

AD

CD

=

4

3

，
∴设CD=3X，则AD=4X．
∵AE：EC=AF：FD=（AD-FD）：FD=2：3，
∴FD=

12

5

X，AF=

8

5

X．
∵AF：AD=EF：CD=2：5，
∴EF=

6

5

X．
∴tan∠ADE=

EF

FD

=

1

2

．
故选C．

点评：此题考查等腰三角形的性质及三角函数的定义．