题目内容
17. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于点M和N;
②作直线MN,分别交AB,BC于点D和E,连接CD.
(1)直线MN垂直平分线段BC吗?请说明理由.
(2)若D是AB的中点,且∠B=35°,求∠A的度数.
分析 (1)根据线段的垂直平分线的定义,只要证明点M、点N在线段BC的垂直平分线上即可;
(2)求出∠ADC,再根据等腰三角形的性质即可解决问题;
解答 解:(1)∵MN垂直平分线段BC.
理由:连接BM、BN、MC、NC.
由作图可知:BM=CM=BN=CN,
∴点M、点N在线段BC的垂直平分线上,
∴MN垂直平分线段BC.
(2)∵MN垂直平分BC,
∴CD=BD,
∴∠DCB=∠B,
∵∠ABC=35°,
∴∠DCB=35°,
∴∠BDC=180°-35°-35°=110°,
∴∠ADC=70°,
∵D是AB中点,
∴BD=DA,
∴CD=DA,
∴∠A=∠ACD=$\frac{180°-70°}{2}$=55°
点评 本题考查线段的垂直平分线的作法、线段垂直平分线的性质等、等腰三角形的性质知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
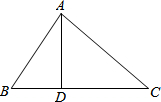 如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.
如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=15,BD=5.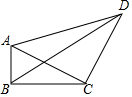 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$. 如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9. 如图是由12个边长为1的小正方形拼成的,请连结这些小正方形的两个顶点,得到一个长为5的线段.
如图是由12个边长为1的小正方形拼成的,请连结这些小正方形的两个顶点,得到一个长为5的线段.