题目内容
3.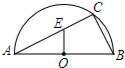 如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )
如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )| A. | $\frac{5}{4}$ | B. | $\frac{7}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
分析 由AB为直径,根据直径所对的圆周角为直角,得到∠C=90°,再根据勾股定理得到AC=8,易证△AOE∽△ACB,得出对应边成比例求出AE,即可得出CE的长.
解答 解:∵AB为直径,
∴∠C=90°,
∵AB=10,BC=6,
∴OA=5,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
又∵OE⊥AB,
∴∠AOE=90°=∠C,
又∵∠OAE=∠CAB,
∴△AOE∽△ACB,
∴$\frac{AE}{AB}=\frac{OA}{AC}$,即$\frac{AE}{10}=\frac{5}{8}$,
解得:AE=$\frac{25}{4}$,
∴CE=AC-AE=8-$\frac{25}{4}$=$\frac{7}{4}$;
故选:B.
点评 本题考查了圆周定理、勾股定理以及相似三角形的判定与性质;熟练掌握圆周角定理,证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某演出小分队是由20名年龄在25岁到30岁的演员组成,请根据表格中提供的数据,(其中28岁和29岁的人数未知),试写出这20名演员年龄的众数的所有可能值26、28、29.
| 年龄(岁) | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(名) | 2 | 5 | 4 | 3 |
13.-2的绝对值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | -|2| |

 ,则sinA=__.
,则sinA=__.
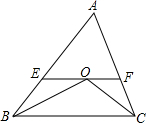 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,若BE=8,CF=6,求EF的值.
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,若BE=8,CF=6,求EF的值.