题目内容
12.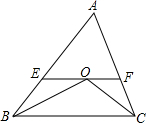 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,若BE=8,CF=6,求EF的值.
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,若BE=8,CF=6,求EF的值.
分析 利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠OBE=∠EOB,∠OCF=∠COF,那么利用等角对等边可得线段的相等,再利用等量代换可求得EF=BE+CF.
解答 解:∵BO平分∠ABC,
∴∠EBO=∠OBC;
∵CO平分∠ACB,
∴∠FCO=∠OCB;
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB;
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴OE=EB,OF=FC;
∵BE=8,CF=6,
∴EF=14.
点评 本题考查了角平分线性质、平行线性质、以及等角对等边的性质等,进行线段的等量代换是正确解答本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
3.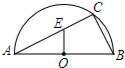 如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )
如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )
 如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )
如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过O作OE⊥AB交AC于点E,则CE的长为( )| A. | $\frac{5}{4}$ | B. | $\frac{7}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
20.已知:当x=2时,多项式x4-bx2+c的值为2016,当x=-2时,多项式x4-bx2+c的值为( )
| A. | -2016 | B. | -2015 | C. | 2016 | D. | 2015 |
7.-5的绝对值等于( )
| A. | -5 | B. | 5 | C. | ±5 | D. | 0 |