题目内容
18．已知△ABC∽△DEF，若△ABC与△DEF的面积的比为4：9，则△ABC与△DEF周长的比为2：3．分析 根据相似三角形的性质求出边长之比，即可求出周长之比．
解答 解：∵△ABC∽△DEF，△ABC与△DEF的面积的比为4：9，
∴△ABC和△DEF的边长的比为2：3，
∴△ABC与△DEF周长的比为2：3，
故答案为：2：3．
点评 本题考查了相似三角形的性质的应用，能熟记相似三角形的性质是解此题的关键，注意：相似三角形的面积之比等于相似比的平方，相似三角形的周长之比等于相似比．
练习册系列答案
名校课堂系列答案
相关题目
13．下列哪个点位于平面直角坐标系的第二象限（ ）
| A． | （2，3） | B． | （2，-3） | C． | （-2，3） | D． | （-2，-3） |
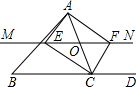如图，在△ABC中，O是AC上一动点（不与点A、C重合），过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
作三角形关于点成中心对称的图形：已知△ABC和点O，画出△DEF，使△DEF与△ABC关于O成中心对称．