题目内容
【题目】已知:如图,![]() 是
是![]() 的外接圆,且
的外接圆,且![]() ,
,![]() ,
,![]() 是
是![]() 的切线,
的切线,![]() 为切点,割线
为切点,割线![]() 过圆心,交
过圆心,交![]() 于另一点
于另一点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的半径及
的半径及![]() 的长.
的长.
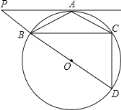
【答案】(1)证明见解析;(2) DC=23.8.
【解析】
(1)如图;由AB=AC,可以得到∠1=∠2,然后利用弦切角定理就可以证得PA与BC的内错角相等,由此得证;
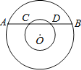
(2)本题需构建直角三角形求解,连接OA,交BC于G,由垂径定理知:OA垂直平分BC,
在Rt△ABG中,已知了AB、BG的长,根据勾股定理可求出AG的长,
在Rt△OBG中,用圆的半径表示出OG的长,然后根据勾股定理,求出圆的半径长,进而可求出OG的长,
△BCD中,易证得OG是△BCD的中位线,由此可求出CD的长.
解:![]() ∵
∵![]() 是
是![]() 的切线,
的切线,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ;
;
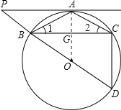
由![]() 可知,
可知,![]() ,
,
∴![]() .
.
∴![]() 为
为![]() 的中点,
的中点,
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目