题目内容
19．已知⊙O的半径r=$\sqrt{3}$，圆外一点P到圆心的距离PO=2，则两条切线PA、PB的夹角的度数是120°．分析 首先根据题意画出图形，然后由⊙O的半径r=$\sqrt{3}$，圆外一点P到圆心的距离PO=2，求得∠APO的度数，然后由切线长定理，求得答案．
解答 
解：如图，连接OA，
∵PA与PB是⊙O的两条切线，
∴OA⊥PA，∠APB=2∠APO，
∵半径r=$\sqrt{3}$，PO=2，
∴sin∠APO=$\frac{OA}{OP}$=$\frac{\sqrt{3}}{2}$，
∴∠APO=60°，
∴∠APB=2∠APO=120°．
故答案为：120°．
点评 此题考查了切线的性质以及切线长定理．注意利用三角函数求得∠APO的度数是关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
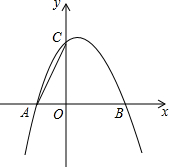如图，二次函数y=-x2+bx+c的图象与x轴交于点A（-1，0），B（2，0），与y轴相交于点C．
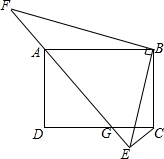如图，在矩形ABCD中，AB=4，BC=3，G是CD边上的动点（点G不与点C、D重合），CE⊥AG的延长线于G点，BF⊥BE交EA的延长线于F点．