题目内容
 如图,四边形ABCD中,AC⊥BD,求证:BC+AD>AB+CD.
如图,四边形ABCD中,AC⊥BD,求证:BC+AD>AB+CD.考点:全等三角形的判定与性质,三角形三边关系
专题:证明题
分析:在OD上截取OB'=OB,在OC上截取OC'=OA,连接C'B',DC',CB',设CB',DC'交于点E,易证△ABO≌△C'B'O可得AB=B'C',易证△DOA≌△DOC'可得AD=DC',易证△COB≌△COB'可得BC=B'C,根据三角形三边关系即可求得CB'+DC'>AB+CD即可解题.
解答:解:在OD上截取OB'=OB,在OC上截取OC'=OA,连接C'B',DC',CB',设CB',DC'交于点E(如图),

在△ABO和△C'B'O中,
,
∴△ABO≌△C'B'O(SAS),
∴AB=B'C',
在△DOA和△DOC'中,
,
∴△DOA≌△DOC'(SAS),
∴AD=DC',
在△COB和△COB'中,
,
∴△COB≌△COB'(SAS),
∴BC=B'C,
∵在△B'C'E中,B'E+C'E>B'C',①
在△CDE中,CE+DE>CD,②
①+②得:CE+C'E+DE+B'E>B'C'+CD,
∴CB'+DC'>AB+CD,
∴BC+AD>AB+CD.

在△ABO和△C'B'O中,
|
∴△ABO≌△C'B'O(SAS),
∴AB=B'C',
在△DOA和△DOC'中,
|
∴△DOA≌△DOC'(SAS),
∴AD=DC',
在△COB和△COB'中,
|
∴△COB≌△COB'(SAS),
∴BC=B'C,
∵在△B'C'E中,B'E+C'E>B'C',①
在△CDE中,CE+DE>CD,②
①+②得:CE+C'E+DE+B'E>B'C'+CD,
∴CB'+DC'>AB+CD,
∴BC+AD>AB+CD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证三对三角形全等是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
A、
| ||||||
| B、-0.216的立方根没有意义 | ||||||
C、-
| ||||||
D、
|
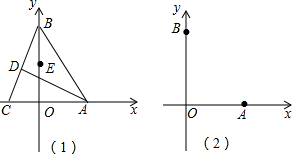
 如图,△ABC中,∠ACB=90°,P是AC的中点,过点A作AD⊥BP于点E,交BC的延长线于点D.若∠DBE=30°,BE=10,求PE,PB的长.
如图,△ABC中,∠ACB=90°,P是AC的中点,过点A作AD⊥BP于点E,交BC的延长线于点D.若∠DBE=30°,BE=10,求PE,PB的长.