题目内容
7. 如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.(1)DQ=10米时,求△APQ的面积.
(2)当DQ的长为多少米时,△APQ的面积为1600平方米.
分析 (1)由DC∥AP,得到$\frac{QD}{AQ}$=$\frac{CD}{AP}$,代入数据求得AP=90,于是得到结论;
(2)设DQ=x米,则AQ=x+20,根据平行线分线段成比例定理得到$\frac{QD}{QA}$=$\frac{DC}{AP}$,得到方程$\frac{x}{x+20}$=$\frac{30}{AP}$,求出AP=$\frac{30(x+20)}{x}$,解一元二次方程即可得到结论.
解答 解:(1)∵DC∥AP,
∴$\frac{QD}{AQ}$=$\frac{CD}{AP}$,
∴$\frac{10}{30}$=$\frac{30}{AP}$,
∴AP=90,
∴S△APQ=$\frac{1}{2}$AQ•AP=1350米2;
(2)设DQ=x米,则AQ=x+20,
∵DC∥AP,
∴$\frac{QD}{QA}$=$\frac{DC}{AP}$,
∴$\frac{x}{x+20}$=$\frac{30}{AP}$,
∴AP=$\frac{30(x+20)}{x}$,
由题意得 $\frac{1}{2}$×$\frac{30(x+20)}{x}$×(x+20)=1600,
化简得3x2-200 x+1200=0,
解x=60或$\frac{20}{3}$.
经检验:x=60或$\frac{20}{3}$是原方程的根,
∴DQ的长应设计为60或$\frac{20}{3}$米.
点评 本题考查了平行线分线段成比例,求三角形的面积,一元二次方程的应用,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
17. 如图,⊙O的直径AB为10cm,弦AC为6cm,则BC=( )
如图,⊙O的直径AB为10cm,弦AC为6cm,则BC=( )
 如图,⊙O的直径AB为10cm,弦AC为6cm,则BC=( )
如图,⊙O的直径AB为10cm,弦AC为6cm,则BC=( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 2$\sqrt{34}$cm |
 如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.
如图,等边△ABC内接于⊙O,AD是直径,则∠CBD=30°.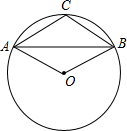 如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.
如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.