题目内容
12.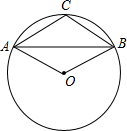 如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.
如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.
分析 如图,连接CO交AB于点E,在圆O上取一点D,连接AD、BD.由“平行四边形的对角相等”推知∠AOB=∠C;然后根据“圆内接四边形的对角互补”求得∠D+∠C=180°;最后由圆周角定理、等量代换求得∠AOB+$\frac{1}{2}$∠AOB=180°.
解答 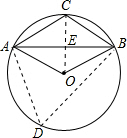 解:如图,连接CO交AB于点E,在圆O上取一点D,连接AD、BD.
解:如图,连接CO交AB于点E,在圆O上取一点D,连接AD、BD.
∵四边形AOBC是平行四边形,OA=OB,
∴平行四边形AOBC为菱形,
∴AB⊥OC.
∵OC是半径,
∴BE=$\frac{1}{2}$AB.
又∵∠D=$\frac{1}{2}$∠AOB,∠ACB+∠D=180°,
∴∠AOB+$\frac{1}{2}$∠AOB=180°,
∴∠AOB=120°,
∴∠BOE=60°,
在Rt△BOE中,BE=OB•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
则AB=2BE=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了菱形的判定与性质,垂径定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2.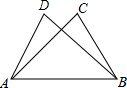 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
20.若|a|=|-4|,则a的值是( )
| A. | 4 | B. | ±4 | C. | -4 | D. | -8 |
 如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.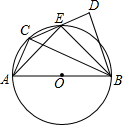 已知如图,AB为⊙O的直径,C为⊙O上的一点且AC=4,BC=8,以BC为底边作等腰直角△BCD,边CD交⊙O于E.
已知如图,AB为⊙O的直径,C为⊙O上的一点且AC=4,BC=8,以BC为底边作等腰直角△BCD,边CD交⊙O于E.