题目内容
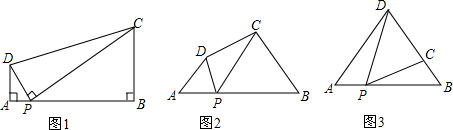
8.(1)问题如图1,在四边形ABCD中,点P为AB 上一点,当∠DPC=∠A=∠B=90°时,求证:AD•BC=AP•BP.
(2)探究
如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=α时,上述结论是否依然成立?说明理由.
(3)应用
请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
分析 (1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)由∠DPC=∠A=∠B=α可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4,则有BC=5-4=1.易证∠DPC=∠A=∠B.根据AD•BC=AP•BP,就可求出t的值.
解答 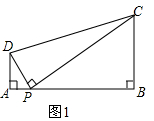 (1)证明:如图1,
(1)证明:如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP;
(2)结论AD•BC=AP•BP仍成立;
理由:如图2,∵∠BPD=∠DPC+∠BPC,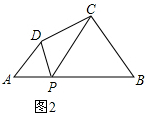
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=α,
∴∠BPC=∠APD,
又∵∠A=∠B=α,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP;
(3)解:如图3,过点D作DE⊥AB于点E,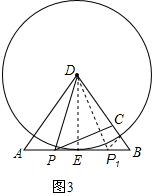
∵AD=BD=5,AB=6,
∴AE=BE=3
∴DE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5-4=1,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得AD•BC=AP•BP,
又∵AP=t,BP=6-t,
∴t(6-t)=5×1,
∴解得:t1=1,t2=5,
∴t的值为1秒或5秒.
点评 本题考查了相似三角形的判定与性质、切线的性质、等腰三角形的性质、勾股定理、三角形外角的性质、解一元二次方程等知识,培养学生运用已有经验解决问题的能力,渗透了特殊到一般的思想.

 若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )| A. | 4 | B. | 4.5 | C. | 5 | D. | 5.5 |
| A. | a+3>0 | B. | a-3<0 | C. | 3a>0 | D. | a3>0 |
| A. | 不等式x<5的整数解有无数多个 | B. | 不等式-2x<8的解集是x<-4 | ||
| C. | 不等式x>-5的负整数解是有限个 | D. | -40是不等式2x<-8的一个解 |
 如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.