题目内容
8. 解决问题:
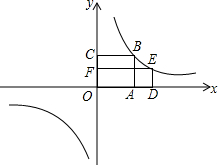
解决问题:如图,在平面直角坐标系中,正方形ABCO的一个顶点在原点,顶点A、C分别在x轴、y轴正半轴上,面积等于8,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象过正方形ABCO的顶点B,E点是y=$\frac{k}{x}(k≠0)$图象上异于B点的任意一点,过E作ED垂直x轴于点D,作EF垂直y轴于F.
(1)求反比例函数的解析式;
(2)当E点在第一象限,且A、D、B、C四点围成的四边形是平行四边形时,求E点的坐标;
(3)设E点的横坐标为a,A、D、B、C四点围成的四边形面积为S,求S与a间的函数关系式.
分析 (1)直接根据反比例函数系数k的几何意义求出k的值即可;
(2)先求出BC的长,再由平行四边形的性质即可得出结论;
(3)求出A点坐标,再分a>4$\sqrt{2}$,0<a<4$\sqrt{2}$与a<0三种情况进行讨论.
解答 解:(1)∵正方形ABCO的一个顶点在原点,顶点A、C分别在x轴、y轴正半轴上,面积等于8,
∴k=8,
∴反比例函数的解析式为y=$\frac{8}{x}$;
(2)∵正方形ABCO的面积是8,
∴BC=OA=$\sqrt{8}$=2$\sqrt{2}$.
∵BC∥EF,
∴只有AD=BC时,A、D、B、C四点围成的四边形是平行四边形,
∴AD=4$\sqrt{2}$,
∴E(4$\sqrt{2}$,$\sqrt{2}$);
(3)∵由(2)知,当E(4$\sqrt{2}$,$\sqrt{2}$)时,四边形ADBC是平行四边形,
∴根据点E横坐标a的变化,AD的长度发生变化,BC不变,AD∥BC.
分三种情况讨论梯形的面积S与a的关系:
当a>4$\sqrt{2}$时,S=$\frac{2\sqrt{2}+A-2\sqrt{2}}{2}$×2$\sqrt{2}$=$\sqrt{2}$a(当a=4$\sqrt{2}$时,点A、D重合,此时ADBC不是四边形,且与E异于B矛盾);
当0<a<4$\sqrt{2}$时,S=$\frac{2\sqrt{2}+2\sqrt{2}-a}{2}$×2$\sqrt{2}$=8-$\sqrt{2}$a;
当a<0时,S=$\frac{2\sqrt{2}+2\sqrt{2}-a}{2}$×2$\sqrt{2}$=8-$\sqrt{2}$a,
综上所述,当a>4$\sqrt{2}$时,S=$\sqrt{2}$a;当a<4$\sqrt{2}$时,S=8-$\sqrt{2}$a.
点评 本题考查的是反比例函数综合题,涉及到反比例函数系数k的几何意义、平行四边形的判定与性质、梯形的面积公式等知识,在解答(3)时要注意进行分类讨论.

| A. | 1100 | B. | -1 | C. | 0 | D. | -1100 |
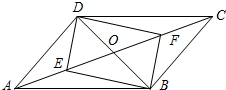 平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动
平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动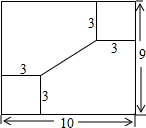 如图,工人师傅准备在一个长,宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.
如图,工人师傅准备在一个长,宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.