题目内容
17.计算(1)$\sqrt{8}$-2cos45°+(7-$\frac{π}{2}$)0-($\frac{1}{2}$)-1+$\sqrt{3}$tan30°
(2)$\sqrt{8}$×sin45°-(${\frac{1}{2}}$)-2+|-3|-$\frac{1}{{\sqrt{2}-1}}$.
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,第四项利用负指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)根据二次根式、特殊角的三角函数值、负整数指数幂、绝对值的意义运算,再根据实数的运算顺序即可得出答案.
解答 解:(1)$\sqrt{8}$-2cos45°+(7-$\frac{π}{2}$)0-($\frac{1}{2}$)-1+$\sqrt{3}$tan30°
=2$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$+1-2+$\sqrt{3}$×$\frac{\sqrt{3}}{3}$
=2$\sqrt{2}$-$\sqrt{2}$+1-2+1
=$\sqrt{2}$;
(2)$\sqrt{8}$×sin45°-(${\frac{1}{2}}$)-2+|-3|-$\frac{1}{{\sqrt{2}-1}}$
=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-4+3-($\sqrt{2}$-1)
=2-4+3-$\sqrt{2}$+1
=2-$\sqrt{2}$.
点评 本题考查了二次根式的混合运算,实数的运算,涉及了二次根式、特殊角的三角函数值、负整数指数幂、绝对值的运算,属于基础题,注意掌握分母有理化的运算.

练习册系列答案
相关题目
8.下列各式中,可分解因式的只有( )
| A. | x2+y2 | B. | x2-y3 | C. | ma+nb | D. | -x2+y2 |
 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1. 如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: 观察如图所示的两个矩形,它们是否相似?请简单说明理由.
观察如图所示的两个矩形,它们是否相似?请简单说明理由.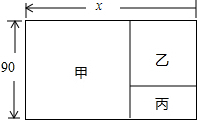 列方程解应用题:如图,有一块长方形土地,长xm,宽90m(x大于90),建筑商把它分成甲、乙、丙三部分,其中甲和乙都是正方形,现在计划甲处修建广场,乙处修建商场,丙处修建住宅.已知丙的面积为1800m2,试求出原长方形土地的面积.
列方程解应用题:如图,有一块长方形土地,长xm,宽90m(x大于90),建筑商把它分成甲、乙、丙三部分,其中甲和乙都是正方形,现在计划甲处修建广场,乙处修建商场,丙处修建住宅.已知丙的面积为1800m2,试求出原长方形土地的面积.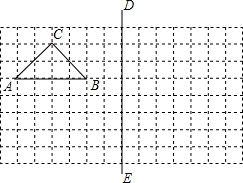 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)