题目内容
5. 已知:如图,∠AEB=∠ADB=90°,C为AB的中点,连接CD、CE、DE,求证:△CDE为等腰三角形.
已知:如图,∠AEB=∠ADB=90°,C为AB的中点,连接CD、CE、DE,求证:△CDE为等腰三角形.
分析 根据直角三角形斜边上中线性质求出CD=CE=$\frac{1}{2}$AB,根据等腰三角形的判定得出即可.
解答 证明:∵在Rt△ADB和Rt△AEB中,∠AEB=∠ADB=90°,C为AB的中点,
∴DC=$\frac{1}{2}$AB,CE=$\frac{1}{2}$AB,
∴CD=CE,
即△CDE是等腰三角形.
点评 本题考查了直角三角形斜边上中线性质,等腰三角形的判定的应用,能运用直角三角形斜边上中线性质进行推理是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
15. 如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
 如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
16.a、b、c为非零实数且满足$\frac{b+c}{a}$=$\frac{a+b}{c}$=$\frac{a+c}{b}$=k,则一次函数y=kx+(1+k)的图象一定经过( )象限.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.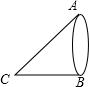 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )| A. | 30米 | B. | 40米 | C. | 50米 | D. | 60米 |
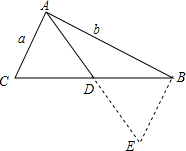 如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.
如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.