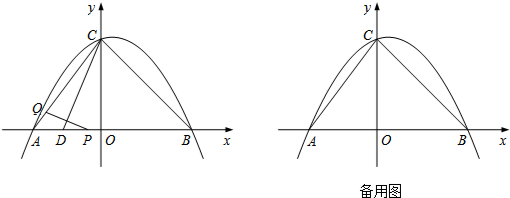题目内容
如图1,抛物线y=ax2+bx+c(a≠0)过O(0,0),A(8,0),B(2,2
)三点,弧AB与OA交于C,弧AB所在的圆的圆心点E,点P是弧AB上一动点.
(1)求这条抛物线的解析式;
(2)若OC=OB,试问点E是否在这条抛物线上?请说明理由;
(3)在(2)的条件下,是否存在这样的位置P和x轴上的一点M,使得△APB与△AMP相似?若存在请求出点M的坐标,若不存在说明理由.

| 3 |
(1)求这条抛物线的解析式;
(2)若OC=OB,试问点E是否在这条抛物线上?请说明理由;
(3)在(2)的条件下,是否存在这样的位置P和x轴上的一点M,使得△APB与△AMP相似?若存在请求出点M的坐标,若不存在说明理由.

考点:二次函数综合题
专题:
分析:(1)抛物线y=ax2+bx+c(a≠0)过O(0,0),A(8,0),B(2,2
)三点,根据待定系数法可求这条抛物线的解析式;
(2)根据中垂线的性质可求点E的坐标为(6,2
),再代入抛物线解析式进行计算即可求解;
(3)存在,△PBA的三个角分别为15°,45°,120°,由E(6,2
).分四种情况:ⅰ.点P是弧BC的中点;ⅱ.连结EP;ⅲ.P(6,-4+2
),B(2,2
);ⅳ.∠PM4A=120°;进行讨论即可求解.
| 3 |
(2)根据中垂线的性质可求点E的坐标为(6,2
| 3 |
(3)存在,△PBA的三个角分别为15°,45°,120°,由E(6,2
| 3 |
| 3 |
| 3 |
解答:解:(1)把O(0,0),代入抛物线解析式y=ax2+bx+c中,得c=0
把A(8,0),B(2,2
),分别代入抛物线解析式y=ax2+bx中,得
解得
.
所以这条抛物线解析式y=-
x2+
x;
(2)∵OC=OB,
∴点C(4.0)
AC的中垂线x=6
BC的中垂线y=
x
则点E的坐标为(6,2
),
当x=6时,y=-
×62+
×6=2
则点E在抛物线上.
 (3)存在,△PBA的三个角分别为15°,45°,120°
(3)存在,△PBA的三个角分别为15°,45°,120°
由E(6,2
).
ⅰ.点P是弧BC的中点,
AM1=AB,
则△APB∽△APM1
AB=8×
=4
OM1=8-4
,
∴M1(8-4
,0)
ⅱ.连结EP,
∠PEA=90°,
AP=4
=
?AM=
=
OM2=8-
,
∴M2(8-
,0)
ⅲ.P(6,-4+2
),B(2,2
)
∠PM3A=45°
OM3=6-(4-2
)=2+2
,
∴M3(2+2
,0)
ⅳ.∠PM4A=120°
OM4=
(4-2
)+6-=4+
,
∴M4(4+
,0)
综上,M1(8-4
,0),M2(8-
,0),M3(2+2
,0),M4(4+
,0).
把A(8,0),B(2,2
| 3 |
|
解得
|
所以这条抛物线解析式y=-
| ||
| 6 |
| 4 |
| 3 |
| 3 |
(2)∵OC=OB,
∴点C(4.0)
AC的中垂线x=6
BC的中垂线y=
| ||
| 3 |
则点E的坐标为(6,2
| 3 |
当x=6时,y=-
| ||
| 6 |
| 4 |
| 3 |
| 3 |
| 3 |
则点E在抛物线上.
 (3)存在,△PBA的三个角分别为15°,45°,120°
(3)存在,△PBA的三个角分别为15°,45°,120° 由E(6,2
| 3 |
ⅰ.点P是弧BC的中点,
AM1=AB,
则△APB∽△APM1
AB=8×
| ||
| 2 |
| 3 |
OM1=8-4
| 3 |
∴M1(8-4
| 3 |
ⅱ.连结EP,
∠PEA=90°,
AP=4
| 2 |
| AM |
| AP |
| AP |
| AB |
(4
| ||
4
|
| 8 | ||
3
|
OM2=8-
8
| ||
| 3 |
∴M2(8-
8
| ||
| 3 |
ⅲ.P(6,-4+2
| 3 |
| 3 |
∠PM3A=45°
OM3=6-(4-2
| 3 |
| 3 |
∴M3(2+2
| 3 |
ⅳ.∠PM4A=120°
OM4=
| ||
| 3 |
| 3 |
4
| ||
| 3 |
∴M4(4+
4
| ||
| 3 |
综上,M1(8-4
| 3 |
8
| ||
| 3 |
| 3 |
4
| ||
| 3 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,中垂线的性质,相似三角形的判定和性质,分类思想的应用,综合性较强,有一定的难度.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F. 如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?
如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?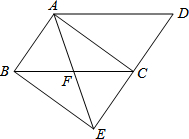 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.