题目内容
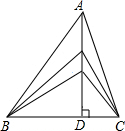 如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.
如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.(1)指出在这个变化过程中的常量和变量;
(2)当高AD从8cm变化到3cm时,求三角形的面积的变化范围;
(3)若三角形的高为x(cm),三角形的面积为y(cm2),写出y与x的关系式.
考点:函数关系式,常量与变量
专题:
分析:(1)由题意根据常量和变量的定义,可得到再点A沿AD所在直线向点D运动时,三角形的面积和高AD发生了变化,底边BC没有发生变化,即可得到常量和变量;(2)由题意可知△ABC的面积=
把AD=8cm和AD=3cm分别代入面积公式,即可得到三角形的面积的变化范围;(3)利用三角形的面积公式即可得到关系式.
| BC•AD |
| 2 |
解答:解:(1)由题意和图形知,
∵在变化过程中线段BC的长度不变,
∴根据常量的定义可知线段BC是常量,
∵点A沿AD所在直线向点D运动,
∴AD的长度在逐渐变短,
∴线段AD是变化的量,
∵高AD变化,所以面积也在变化,
故常量是线段BC,变量为线段AD,因变量是△ABC的面积;
(2)由题意可知
△ABC的面积=
,
把AD=8cm代入,得△ABC的面积=
=40cm2,
把AD=3cm代入,得△ABC的面积=
=15cm2,
所以三角形的面积的变化范围为:15cm2≤△ABC的面积≤40cm2;
(3)∵△ABC的面积=
,
∴y=
=5x,
所以y与x的关系式为:y=5x.
∵在变化过程中线段BC的长度不变,
∴根据常量的定义可知线段BC是常量,
∵点A沿AD所在直线向点D运动,
∴AD的长度在逐渐变短,
∴线段AD是变化的量,
∵高AD变化,所以面积也在变化,
故常量是线段BC,变量为线段AD,因变量是△ABC的面积;
(2)由题意可知
△ABC的面积=
| BC•AD |
| 2 |
把AD=8cm代入,得△ABC的面积=
| 10×8 |
| 2 |
把AD=3cm代入,得△ABC的面积=
| 10×3 |
| 2 |
所以三角形的面积的变化范围为:15cm2≤△ABC的面积≤40cm2;
(3)∵△ABC的面积=
| BC•x |
| 2 |
∴y=
| 10x |
| 2 |
所以y与x的关系式为:y=5x.
点评:本题主要考查了函数关系式,常量与变量,函数值及三角形的面积,解题的关键是能求出y与x的关系式.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA•PB的值是( )
如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA•PB的值是( )| A、16 | B、16π | C、4 | D、4π |
若
=
,那么a:b的值是( )
| a+b |
| a |
| 5 |
| 3 |
| A、3:2 | B、2:3 |
| C、C、3:5 | D、D、5:3 |
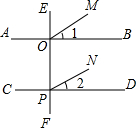 如图,EF⊥AB,垂足为O,EF⊥CD,垂足为P,且∠1=∠2,说出OM与PN的位置关系,并说明理由.
如图,EF⊥AB,垂足为O,EF⊥CD,垂足为P,且∠1=∠2,说出OM与PN的位置关系,并说明理由.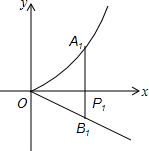 如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交
如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交 如图,直线AB、CD相交于点O,DM⊥AB,若∠1=∠2,求∠CON的度数.
如图,直线AB、CD相交于点O,DM⊥AB,若∠1=∠2,求∠CON的度数. 有理数a,b在数轴上(如图),那么
有理数a,b在数轴上(如图),那么 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.