题目内容
1.已知抛物线y=x2-2kx-3,当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,则k=1.分析 因为当x>1时、y随x的增大而增大,当x<1时、y随x的增大而减小;所以x=1是抛物线y=x2-2kx-3的对称轴,即-$\frac{-2k}{2}$=1,可解得k.
解答 解:∵抛物线y=x2-2kx-3,当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,
∴x=1是抛物线y=x2-2kx-3的对称轴,
即-$\frac{-2k}{2}$=1,
解得k=1.
故答案为:1.
点评 此题考查二次函数的性质,利用抛物线的对称轴求出抛物线的系数是解决问题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
12.已知直角三角形的两直角边长分别是4和6,则其斜边长是( )
| A. | 4 | B. | 6 | C. | 10 | D. | 2$\sqrt{13}$ |
16.已知二次函数y=-x2+4x-a(a为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程-x2+4x-a=0的两实数根是( )
| A. | x1=1,x2=-1 | B. | x1=1,x2=2 | C. | x1=1,x2=0 | D. | x1=1,x2=3 |
6.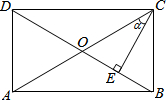 如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
 如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 2 |
7.⊙O的直径是3,直线l与⊙O相交,圆心O到直线l的距离是d,则d应该满足( )
| A. | d>3 | B. | 1.5<d<3 | C. | 0≤d<3 | D. | 0≤d<1.5 |
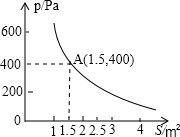 某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示
某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示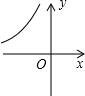 如图,点P是双曲线y=-$\frac{{9\sqrt{3}}}{x}$(x<0)上动点,在y轴上取点Q,使得以P、Q、O为顶点的三角形是含有60°角的直角三角形,则符合条件的点Q的坐标是(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$).
如图,点P是双曲线y=-$\frac{{9\sqrt{3}}}{x}$(x<0)上动点,在y轴上取点Q,使得以P、Q、O为顶点的三角形是含有60°角的直角三角形,则符合条件的点Q的坐标是(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$).