题目内容
9．已知m，n均可取1，2，…，2009之一，则使方程x2-mx+n=0有实根的数对（m，n）的个数为2019043．分析 根据跟的判别式可知：△=m2-4n≥0，分两种情况探讨：m≠n和m=n分析得出答案即可．
解答 解：∵方程x2-mx+n=0有实根，
∴m2-4n≥0，
∴m2≥4n，
当m≠n时，任意两个数满足m＞n，都可以满足条件，满足条件的数对为：$\frac{2008×（2008+1）}{2}$=2017036，
当m=n时，m不能为1，2，3，满足条件的数对为：2009-3=2007，
∴满足条件的总数对为：2017036+2007=2019043．
故答案为2019043．
点评 本题考查了一元二次方程根的情况与判别式的关系：
若△＞0，则有两不相等的实数根；
若△＜0，则无实数根；
若△=0，则有两相等的实数根．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
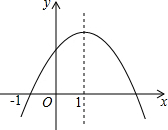二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出下列结论：
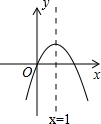二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：（1）b＞0；（2）c＞0；（3）4a+2b+c＞0；（4）（a+b）2＜b2，其中正确的有（ ）
如图，AB是⊙O的直径，C是半圆上的一个三等分点，D是$\widehat{AC}$的中点，P是直径AB上一点，⊙O是半径为1，则PC+PD的最小值是$\sqrt{2}$．