题目内容
7.在Rt△ABC中,∠ACB=90°,sinB=$\frac{5}{13}$,则cosB=$\frac{12}{13}$.分析 根据sin2α+cos2α=1,可得答案.
解答 解:在Rt△ABC中,∠ACB=90°,sinB=$\frac{5}{13}$,得
cosβ=$\sqrt{1-si{n}^{2}β}$=$\sqrt{1-(\frac{5}{13})^{2}}$=$\frac{12}{13}$,
故答案为:$\frac{12}{13}$.
点评 本题考查了同角三角函数关系,利用sin2α+cos2α=1是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
 抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.在下表的空白处填上适当的数,使各横行与各竖列的4个数之和相等.
| 1 | -3 | -4 | 6 |
| -2 | +7 | ||
| 5 | -8 | ||
| -10 | 9 |
17.下列计算中,结果正确的是( )
| A. | a2•a3=a6 | B. | (2x)3=6x3 | C. | a6÷a2=a3 | D. | (a2)3=a6 |
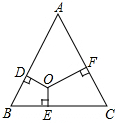 如图,等边三角形ABC的边长为4,高为h.
如图,等边三角形ABC的边长为4,高为h.